1 AdNDP

1.1 优化和频率计算

B4.square.gjf文件：

%nprocshared=16
%mem=16GB
%chk=B4.chk
#p opt freq b3lyp/6-31g 
 
B4
 
0 1
 B                  1.21435106   -0.69628856   -0.10869034
 B                 -0.36399099    1.17989093   -0.17470963
 B                  1.35821264    1.03729467    0.15887841
 B                 -0.51861172   -0.54166004    0.15688456

g09<B4.square.gjf>B4.square.log,生成B4.square.log文件，在ResultsSummary中看总能量，对称性，是否有虚頻。假如有虚頻： Results->Vibrations, 消除虚頻（负频率），产生新的结构，重新优化和计算频率，直到无虚頻。 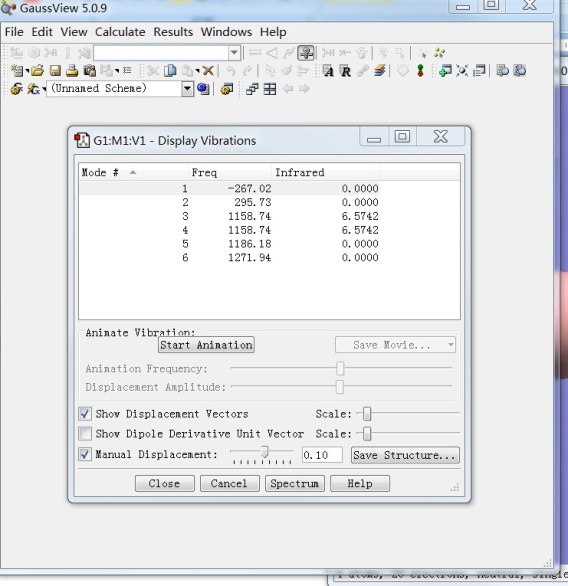Fig. 1: Fequency in Gaussian

1.2 极化，MO及NBO键级计算

B4.nbo.gjf:

%nproc=16
%mem=16GB
%chk=B4.chk
#p b3lyp/6-31g  polar scf=tight pop(full,nboread) density=current
 
B4_NBO
 
0 1
 B                  0.00000000    0.94287500    0.00044800
 B                  0.00000000   -0.94287500    0.00044800
 B                  1.22153200    0.00000000   -0.00044800
 B                 -1.22153200    0.00000000   -0.00044800
 
$NBO DMNAO AONAO BNDIDX archive file=B4.nbo $END

BNDIDX 是NBO键级分析，DMNAO关键词输出的NAO密度矩阵,AONAO为AO到NAO转换，DMNAO和AONAO为AdNDP分析做准备。 g09<B4.nbo.gjf>B4. nbo.log生成B4.nbo.log文件及B4.chk文件，执行fromchk B4.chk B4.fchk, 生成B4.fchk。 B4.nbo.log文件会给出键级分析（使用NBO3.0）不太准，可使用B4.nbo.47文件和NBO高版本进一步分析。 B4.fchk 在Gaussian打开，点击按钮，查看MO轨道。直接保存MO图，或者打开ResultsSurface/Contour, 保存为cube文件，在Molkel可以画出更漂亮的MO轨道图。

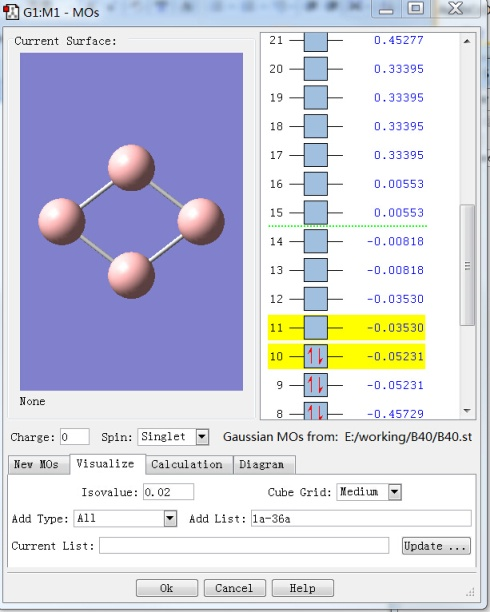
1.3 NBO键级和NRT计算

B4.nbo.47文件修改，初始：

$GENNBO  NATOMS=4  NBAS=36  UPPER  BODM  $END
$NBO  $END
$COORD...

改为：

$GENNBO  NATOMS=4  NBAS=36  UPPER  BODM  $END
$NBO NRT BNDIDX   $END
$COORD...

执行： gennbo B4.nbo B4.nbo.47，生成B4.nbo.nbo 文件，包含键级，自然成键分析，共振结构等。

1.4 ADNDP分析

有两种途径进行AdNDP分析：

1.4.1 Multiwfn

具体分析过程参照： http://emuch.net/html/201205/4484349.html

启动Multiwfn，输入B4.nbo.log的文件路径，然后选主功能14就进入了AdNDP分析模块。Multiwfn会先载入一些NAO信息和以NAO为基的密度矩阵，然后自动扣除内核NAO轨道对密度矩阵的贡献，然后就会看到一堆选项。

由于B4这个体系非常简单，所以只需要用穷举搜索的方法就行了。首先选2去穷举搜索所有单中心轨道，但是没有找到占据数高于阈值的轨道，这也是理所当然，从直觉上就知道B4不可能有孤对电子。当前的阈值就是选项4上显示的值，目前版本中默认为1.7。

接下来再按2，就开始穷举搜索双中心轨道，经过穷举搜索，从菜单前头显示的候选轨道列表中得知发现了4个双中心轨道的占据数都高于阈值，它们的占据数都高达1.97，因此是理想的2c-2e轨道，此时选0,然后输入4，就把这两个轨道从候选列表中取了出来成为AdNDP轨道。继续穷举搜索其它多中心键。（注：当前的候选轨道列表总是自动显示在菜单的前头，为了避免其信息碍事，只有选择5查看AdNDP轨道信息一览表或者选13查看剩余电子分布时没显示出来。但任何时候都可以从中用选项0选取轨道，或者用选项8和10来分别查看它们和导出它们）现在可以选7来观看这两个AdNDP轨道。Multiwfn首先会读取Guassian输出文件中的原始基函数与NAO间的变换矩阵，然后让你输入相应的fch文件的路径，假设你已经把B4.nbo.fchk放到了B4.nbo.log相同的目录下，那么Multiwfn就会直接读取。读取完毕后，你会看到一个图形界面，和Multiwfn主功能0提供的界面一模一样，可以观看分子结构，在右下角选相应的AdNDP轨道编号就能立刻显示出等值面图。（大部分是http://emuch.net/html/201205/4484349.html网页上的原话，呵呵），最终可分析得到4个双中心键和两个4中心键。

1.4.2 AdNDP

使用Boldyrev课题组的adNDP程序。http://ion.chem.usu.edu/~boldyrev/adndp.php

需要文件包括：

DMNAO AONAO 计算得到的B4.nbo.log
另一部分计算B4.cmo.gjf：

%nproc=16
%mem=16GB
%chk=B4_CMO.chk
#p b3lyp/6-31g scf=tight pop(full) density=current gfoldprint

B4_CMO

0 1
 B                  0.00000000    0.94287500    0.00044800
 B                  0.00000000   -0.94287500    0.00044800
 B                  1.22153200    0.00000000   -0.00044800
 B                 -1.22153200    0.00000000   -0.00044800

得到的B4.cmo.log.
3. AdNDP.in:

NBO filename
g09.nbo.log
Number of atoms
4
mount of valence electronic pairs
6
Total amount of electronic pairs
10
Total amount of basis functions
36
Amount of basis functions on each atom
9
9
9
9
Occupation number thresholds
0.1 
0.1
0.1
0.1
0.1
0.1
CMO filename
B4.cmo.log

执行 AdNDP.exe, 生成NDP_g09.nbo.log，内容

NBOAmnt= 10
 1  1 0 0 0 Occ   1.99808666
 2  2 0 0 0 Occ   1.99808666
 3  3 0 0 0 Occ   1.99800394
 4  4 0 0 0 Occ   1.99800394
 5  1 3 0 0 Occ   1.97660674
 6  1 4 0 0 Occ   1.97660674
 7  2 3 0 0 Occ   1.97660674
 8  2 4 0 0 Occ   1.97660674
 9  1 2 3 4 Occ   2.00009936
 10  1 2 3 4 Occ   1.99993854
（键序号 涉及电子nc-2e 还有占据数ON）
...
 Residual Density  0.1012

还有重写系数的B4.cmo.log文件用来画AdNDP分布。

2 光电子谱的计算(应该更高精度)

B4.pes.gjf:

%nproc=16
%mem=16GB
%chk=B4.chk
#p b3lyp/6-31g  td=(nstates=6,50-50) scf=direct

B4_pes

0 1
 B                  0.00000000    0.94287500    0.00044800
 B                  0.00000000   -0.94287500    0.00044800
 B                  1.22153200    0.00000000   -0.00044800
 B                 -1.22153200    0.00000000   -0.00044800

得到B4.pes.log,其中：

Excited State   1:      Triplet-A1     0.9964 eV 1244.32 nm  f=0.0000  <S**2>=2.000
      10 -> 11         0.77272
      10 <- 11         0.32512
 This state for optimization and/or second-order correction.
 Total Energy, E(TD-HF/TD-KS) =  -99.0666868570    
 Copying the excited state density for this state as the 1-particle RhoCI density.
 
 Excited State   2:      Triplet-B1     1.0373 eV 1195.27 nm  f=0.0000  <S**2>=2.000
       6 -> 11        -0.10739
      10 -> 12         0.79424
      10 <- 12         0.38004
 
 Excited State   3:      Triplet-A2     2.3791 eV  521.15 nm  f=0.0000  <S**2>=2.000
       7 -> 12        -0.10146
       9 -> 11         0.70106
 
 Excited State   4:      Triplet-B2     2.5560 eV  485.08 nm  f=0.0000  <S**2>=2.000
       7 -> 11        -0.20588
       9 -> 12         0.66845
      10 -> 15        -0.13883
 
 Excited State   5:      Triplet-A1     2.6993 eV  459.32 nm  f=0.0000  <S**2>=2.000
       8 -> 11         0.70544
 
 Excited State   6:      Triplet-B1     2.8709 eV  431.86 nm  f=0.0000  <S**2>=2.000
       8 -> 12         0.52131
      10 -> 13         0.48849
 
 Excited State   7:      Singlet-A2     3.0647 eV  404.56 nm  f=0.0000  <S**2>=0.000
       9 -> 11         0.70678
 
 Excited State   8:      Singlet-A1     3.2895 eV  376.91 nm  f=0.0000  <S**2>=0.000
      10 -> 11         0.70664
      10 <- 11        -0.10324
 
 Excited State   9:      Singlet-A1     3.3287 eV  372.47 nm  f=0.0009  <S**2>=0.000
       8 -> 11         0.70616
 
 Excited State  10:      Singlet-B2     3.4810 eV  356.17 nm  f=0.0062  <S**2>=0.000
       9 -> 12         0.70151
 
 Excited State  11:      Singlet-B1     3.5350 eV  350.73 nm  f=0.0000  <S**2>=0.000
       8 -> 12         0.69476
      10 -> 13        -0.13252
 
 Excited State  12:      Singlet-B1     3.6670 eV  338.11 nm  f=0.0952  <S**2>=0.000
       8 -> 13        -0.31591
      10 -> 12         0.62960

3 Basis Functions

https://chem.libretexts.org/Textbook_Maps/Physical_and_Theoretical_Chemistry_Textbook_Maps/Map%3A_Physical_Chemistry_(McQuarrie_and_Simon)/11%3A_Computational_Quantum_Chemistry/11.1%3A_Gaussian_Basis_Sets

3.1 Slater Type Orbitals (STOs)

R(r)=Nr^{n − 1}e^{−\zeta r} where

n is a natural number that plays the role of principal quantum number, n = 1,2,…,
N is a normalizing constant,
r is the distance of the electron from the atomic nucleus, and \zeta is a constant related to the effective charge of the nucleus, the nuclear charge being partly shielded by electrons. Historically, the effective nuclear charge was estimated by Slater’s rules.

3.2 Double-zeta basis Sets

R_{2s}(r)=C_1re^{-\zeta _1r}+C_2re^{-\zeta _2 r}

3.3 Gaussian Orbitals

G_{nlm}(r,\theta,\psi)=N_nr^{n-1}e^{-\alpha r^2}Y^m_l(\theta,\psi)

Table: Different Gaussian Basis sets
Basis	Num	Basis	Num	Basis	Num
STO-3G	5	6-31G	9	6-311G	13
3-21G	9	6-31G*	15	6-311G*	18*
4-31G	9	6-31+G	19	6-311+G*	22*