1 Binding Energy and Curvature energy

1. Average binding energy $E_b[AB]=(N_A*E_A+N_B*E_B-E_{tot}[AB])/(N_A+N_B)$ where $E_A$ and $E_B$ are the energy of free atom in vacuum for A and B.
2. ^[1,2]Curvature energy for nanotubes $E_{tube}=E_{2D}-E_{curv}=E_{2D}-A/R^2$

2 Formation Energy

1. ^[3]General trend in formation energy for QD: $\varepsilon(n)-\varepsilon(\infty)\propto const/\sqrt{n}$

2.1 formation energy of a defect or impurity

2. ^[4]The formation energy of a defect or impurity X in charge state q is defined as $E_f[X^q]=E_{tot}[X^q]-E_{tot}[GaN,bulk]-\sum\limits_i n_i\mu_i+q[E_F+E_\nu+{\Delta}V]$ $E{tot}[X]$ is the total energy derived from a supercell calculation with one impurity or defect X in the cell, and $E_{tot}[GaN,bulk]$ is the total energy for the equivalent supercell containing only bulk GaN. $n_i$ indicates the number of atoms of type i (host atoms or impurity atoms) that have been added to ($n_i>0$) or removed from ($n_i<0$) the supercell when the defect or impurity is created, and the $\mu_i$ are the corresponding chemical potentials of these species. E~F ~ is the Fermi level, referenced to the valence-band maximum in the bulk. Due to the choice of this reference, we need to explicitly put in the energy of the bulk valence-band maximum, $E_{\nu}$, in our expressions for formation energies of charged states. As discussed in Sec. II C, we also need to add a correction term DV, to align the reference potential in our defect supercell with that in the bulk.

• In GaN: $\mu_{Ga}+\mu_N=E_{tot}[GaN]$
• extreme Ga-rich conditions: $\mu_{Ga}=\mu_{Ga[bulk]},\mu_N^{min}=E_{tot}[GaNs]-\mu_{Ga[bulk]}$
• extreme N-rich conditions: $\mu_N=\mu_{N[N2]},\mu_{Ga}^{min}=E_{tot}[GaN]-\mu_{N[N2]}$ The total energy of GaN can also be expressed as $E_{tot}[GaN]=\mu_{{Ga}[bulk]}+\mu_{N[N_2]}+{\Delta}H_f[GaN]$ where ${\Delta}H_f[GaN]$ is the enthalpy of formation, which is negative for a stable compound.

2.2 Chemical Potential

The chemical potentials can in principle be related to partial pressures, using standard thermodynamic expressions. For instance, the chemical potential for hydrogen atoms in a gas of H2 molecules is given by $2\mu_H=E_{H_2}+k_BTln(\frac{pV_Q}{k_BT}-lnZ_{rot}-lnZ_{vib})$ where E_H2 is the energy of an H2 molecule, k_B is the Boltzmann constant, T is the temperature, and p is the pressure. $V_Q=(h^2/2\pi m k_B T)^{3/2}$ is the quantum volume, and Z_rot and Z_vib are the rotational and vibrational partition functions.

2.3 Helmholtz free energy^[5]

From the computed phonon spectrum of the sheet configurations, the temperature-dependent vibrational Helmholtz free energy and entropy can be calculated in the harmonic approximation²¹.
$F(V,T)$, the free energy of a crystal, can be written as a sum of $E(V)$, the energy of the static lattice at the equilibrium configuration, and $F_{vib}(V, T)$, the vibrational free energy associated with the modes, $\omega(q)$. $F=E+F_{vib}=E+\sum_q\frac{\hbar\omega(q)}{2}-ST$ Here, S is entropy, $\sum_q\frac{\hbar\omega(q)}{2}$ is the summation of contributions of the zero-point energy from each phonon mode, and T is the temperature.
Considering the first-order corrections to be small, S can be calculated²⁰ as follows: $S=-k_B\sum_q ln(1-\exp(-\hbar\omega(q)/k_BT))$ The lattice heat capacity per unit cell at constant volume can be defined as follows: $C_V(T)=\sum_q{c_v(q)}=k_B\sum_q{({\hbar}{\omega}(q)/2K_BT)^2/sinh^2({\hbar}{\omega}(q)/2K_BT)}$

2.4 Formation Valley^[6]

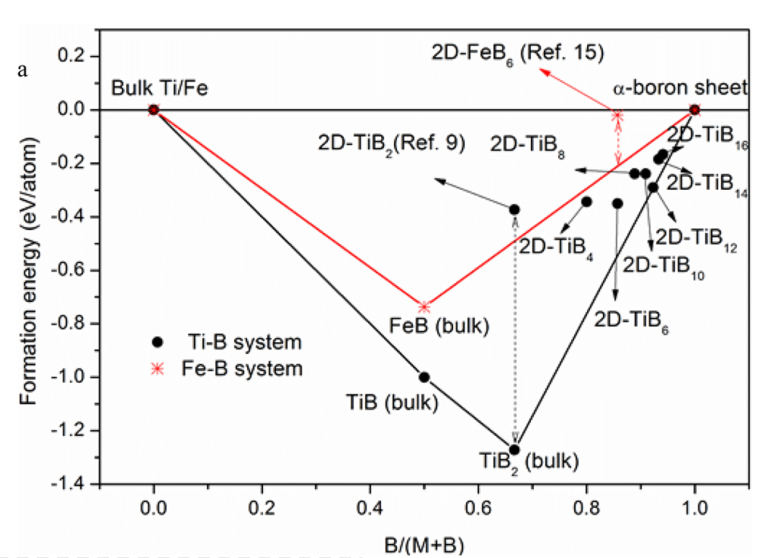
Formation energies per atom (E_f) for 2D TiB_x-multilayers. $E_f=(E_{TiB_x}-E_{Ti}-xE_B)/(x+1)$ from alloy, bulk Ti and $\alpha$ sheet.

2.5 Surface Energy

• Thick engough，surface energy $\gamma$ vs. thickness convergence test needed

$\gamma=\frac{E_{slab}-N*E_{bulk}}{2A}$, where $E_{slab}$ is the total energy of surface slab obtained using density functional theory. N is the number of atoms in the surface slab. $E_{bulk}$ is the bulk energy per atom. A is the surface area. For a slab, we have two surfaces and they are of the same type, which is reflected by the number 2 in the denominator. To guarantee this, we need to create the slab carefully to make sure that the upper and lower surfaces are of the same type.