1 Sabatier Principle

It states that a good catalyst material should bind the molecules that participate in the chemical reaction neither too strongly nor too weakly to its surface. The bonds should be strong enough to activate the molecules for the reaction, but still weak enough to not hold on to them forever. Unfortunately, many materials follow so-called scaling relations. They tend to bind different molecules either all stronger or all weaker, while for many reactions catalysts are needed that selectively bind certain molecules stronger and others weaker.

2 Zero point energy corrections and entropic contributions to the free energies^[1].

Table: Zero point energy corrections and entropic contri- butions to the free energies.
Group	TS(eV)	T{\Delta}S	E_{ZPE}	{\Delta}E_{ZPE}
H2O(0.035bar)	0.67	0	0.56	0
*OH+1/2H₂	0.20	-0.47	0.44	-0.12
*O+H₂	0.41	-0.27	0.34	-0.22
1/2O₂+H₂	0.73	0.05	0.32	-0.24
H2	0.41		0.27
1/2O₂	0.32		0.05
O*	0		0.07
OH*	0		0.30
H*	0		0.17

3 Hydrogen-evolution reaction (HER)

3.1 Mechanism of hydrogen evolution reactions in acidic and alkaline solution

3.1.1 Acidic electrolyte

2H(aq)^++2e^-{\rightarrow}H_2(g)

Volmer step: H^++e^-{\rightarrow}H_{ads}
Tafel step: 2H_{ads}{\rightarrow}H_2
Heyrovsky step: H^++H_{ads}+e^-{\rightarrow}H_2
整个反应的速率很大程度上取决于氢吸附自由能\Delta G_H如果氢气与表面键合太弱，吸附（Volmer）步骤将限制整个反应速率，而如果键合太强，解吸（Heyrovsky/Tafel）步骤将限制反应速率。因此，具有HER活性的催化剂的必要不充分条件是\Delta G_H \approx 0。

3.1.2 Alkaline electrolyte

2H_2O+2e^-{\rightarrow}H_2(g)+2OH(aq)^-

Volmer step: 2H_2O+e^-{\rightarrow}2H_{ads}+2OH^-
Tafel step: 2H_{ads}{\rightarrow}H_2
Heyrovsky step: H_2O+H_{ads}+e^-{\rightarrow}H_2+OH^-

3.2 HER calculation method^[2–4]

The electrocatalytic activity of a given material for HER can be closely correlated to the adsorption energy of a single H atom on the surface of the material. According to basic Sabatier principle, with the free energy of adsorbed H on the catalyst usually required to be close to that of the product. Therefore, the value of free energy of H* (\Delta G_{H*}) of a site is usually viewed as a reliable indicator of the degree of catalytic activity of the site in question toward HER, where a smaller absolute value of \Delta G_{H*} means a better catalytic activity toward HER.^[1]

The related free energies can be computed by the formula \Delta G_{H*}=\Delta E_{H*}-\Delta ZPE-T\Delta S, in which \Delta E_{H*}, \Delta ZPE and \Delta S are the binding energy, zero point energy change and entropy change of H* adsorption, respectively. The differential hydrogen adsorption energy \Delta E_{H*} is defined as follows, {\Delta}E_H*=E_{system+nH}-E_{system+(n-1)H}-1/2E_{H_2}, where E_{system+nH} is the total DFT energy for the system with n hydrogen atoms adsorbed, E_{system+(n-1)H} is the total DFT energy for (n-1) hydrogen atoms adsorbed and E_{H_2} is the DFT energy for a hydrogen molecule in the gas phase. The differential hydrogen binding energy describes the energy needed to increase the coverage by one hydrogen atom. In this work, we computed the T\Delta S and \Delta ZPE according to the scheme proposed by Norskov et al.^[1] Specifically, \Delta S was obtained by using the equation \Delta S=S(H*)-1/2S(H_2)\approx -1/2S^0(H_2), as the configurational and vibrational entropy of H* is negligible. Since TS(H_2) is 0.41 eV for H2 at at standard conditions (298.15 K and 1 atm), the corresponding T\Delta S was obtained to be -0.205 eV. On the other hand, the equation \Delta ZPE=ZPE(H*)-1/2ZPE(H_2)(ZPE(H_2)=0.27eV) was employed to calculate \Delta ZPE for H*. It is worth mentioning here that our computed ZPE(H2) value was about 0.288 eV, close to the value reported by Norskov et al. for a similar system.^[1]

HER1

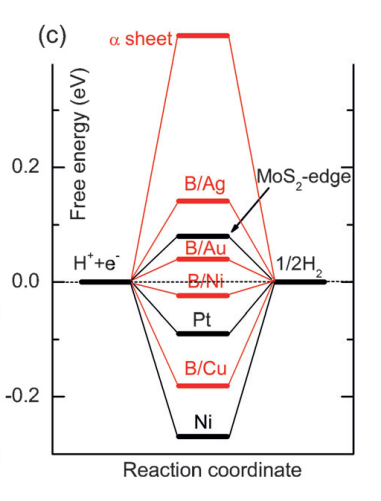
Fig. 2: Free-energy diagram for hydrogen evolution reaction on different catalysts. The free energy of H⁺+ e^- is defined as the same as that of 1/2H₂ at room temperature and standard conditions^[3].

3.2.1 Overpotential

The theoretical overpotential \eta for HER, which is determined by \Delta G_{H^*}: \color{red} \eta=-|\Delta G_{H^*}|/e

4 Oxygen Reduction Reaction(ORR) and Oxygen Evolution Reaction (OER)

1/2O_2+H^++e^-\rightarrow 1/2H_2O_2\ (U_0^{O_2/H_2O_2} =0.7\ V\ vs.\ RHE) 1/4O_2(g)+H^++e^-\rightarrow 1/2H_2O\ (U_0^{O_2/H_2O} =1.229\ V\ vs.\ RHE (pH=0) 1/4O_2(g)+1/2H_2O-\rightarrow OH^-\ (U_0^{O_2/H_2O} =0.41\ V\ vs.\ RHE (pH=14)

4.1 2e-ORR^[5]

The total energy (E) and corresponding thermodynamic quantities, in eV, for free H₂, H₂O, H₂O₂ species, were listed in Supplementary Table 8. Since O₂ molecule is poorly described by standard DFT calculations, all the free energies were calculated by using the free energies of H₂O (l) and H2 (g) as ref.³⁰. The free energies of O2 molecule and H₂O₂ molecules are determined by equilibrium potential of four-electron (1.23 V vs. RHE) and two-electron (0.70 V vs. RHE) ORR, which are estimated by 4.92 (4 × 1.23) and 3.52 (4 × 1.23–0.70 × 2) eV, respectively.
For the two-electron ORR, there are two reaction steps²⁵(in acidic solution) *+O_2+H^++e^-\rightarrow OOH^* \ (5) OOH^*+H^++e^-\rightarrow H_2O_2+*\ (6) For the hydrogenation of oxygen (Eq. (5)), the \Delta G was calculated by Eqs. (7)–(9): \Delta G_1=\mu_{OOH^*}-\mu_*-\mu_{O_2}-1/2\mu_{H_2}\ (7) while for the reduction of OOH* to from H₂O₂ (Eq. (6)), the \Delta G can be obtained directly by Eq. (10): \Delta G_2=-1.4eV-\Delta G_1\ (10) herein, the G(OOH^*) is defined by Eq. (11): G(OOH^*)=4.92eV+\Delta G_1\ (11)

4.2 4e-ORR^[6,7]

4.2.1 Reaction mechanism

The ORR, OER and HER pathways on SAC systems were calculated in detail according to electrochemical framework developed by Nørskov and his co-workers^[8]. As for ORR, in an alkaline electrolyte (pH = 14), H₂O rather than H₃O+ may act as the proton donor, so overall reaction scheme of the ORR can be written as: O_2+2H_2O+4e^-\leftrightarrow 4OH^- (8)
The ORR may proceed through the following elementary steps, which are usually employed to investigate the electrocatalysis of the ORR on various materials(in alkaline solution): O_2(g) + H_2O(l)+e^-+^*\rightarrow OOH^*+OH^-\ (9) OOH^*+e^-\rightarrow O^*+OH^-\ (10) O^*+H_2O(l)+e^-\rightarrow OH^*+OH^-\ (11) OH^*+e^-\rightarrow OH^-+*\ (12) where ^* stands for an active site on the catalytic surface, (l) and (g) refer to liquid and gas phases, respectively.

In acidic solution: O_2(g) + H^++e^-+^*\rightarrow OOH^*\ (17) OOH^* + H^++e^-\rightarrow O^*+H_2O\ (18) O^*+H^++e^-\rightarrow OH^*\ (19) OH^*+H^++e^-\rightarrow H_2O + ^*\ (20)

The OER occurring in an alkaline electrolyte (pH = 14) through elementary steps takes the reverse direction of ORR: OH^-+* \rightarrow OH ^*+e^-\ (13) OH^*+OH^-\rightarrow O^*+H_2O(l)+e^-\ (14) O^*+OH^-\rightarrow OOH^*+e^-\ (15) OOH^*+OH^-\rightarrow O_2(g) + H_2O(l)+e^-+^*\ (16)
As for HER, in an acid electrolyte (pH = 0), H+ can act as the proton donor, so the overall reaction scheme of the HER can be written as: H^++e^-+^*\leftrightarrow 1/2H_2(g)+* where the * represents the adsorption site.

4.2.2 Reaction free energy calculation

For proton-transfer steps, reaction free energies are regarded as approximate values of the activation barriers, because detailed calculations for the transfer of a solvated proton to adsorbed OH− show the neglect of overbarriers has been proven as a very good approximation for a situation where the proton transfer is downhill in energy^[9]. This approximation may result in a slight overestimation of activity for a given proton-transfer elementary step, but can still qualitatively represent the right relative energetic ordering of the various proton-transfer elementary steps. Therefore, we took the reactions in equations (9)–(16) to derive the thermochemistry for ORR and OER. The RHE model developed by Nørskov and co-workers35,60,^[8] was used to obtain the Gibbs reaction free energy of these electrochemical elementary steps. In this model, we set up RHE as the reference electrode, which allows us to replace chemical potential (\mu) of the proton–electron pair with that of half a hydrogen molecule: \mu_{H^+}+ \mu_{e^−} = 1/2\mu_{H_2}, at conditions with U = 0 V and P_{H_2} = 1 bar.
The chemical potential of each adsorbate is defined as: \mu=E+E_{ZPE}-T\times S\ (18) where the E is the total energy obtained from DFT calculations, E_{ZPE} is zero-point energy and S is the entropy at 298 K. In order to obtain the reactionfree energy of each elementary step of ORR, OER and HER, we calculated the adsorption free energy of O, OH, OOH* and H*. Because it is difficult to obtain the exact free energy of OOH, O, OH and H radicals in the electrolyte solution, the adsorption free energy \Delta \mu_{OOH^*}, \Delta \mu_{O^*}, \Delta \mu_{OH^*} and\Delta \mu_{H^*}, are relative to the free energy of stoichiometrically appropriate amounts of H₂O (g) and H2(g), defined as follows: \color{red} {\Delta}G_{O^*}={\Delta}G(H_2O(l)+*\rightarrow O^*+H_2(g) \color{red} =\mu_{O^*}+\mu_{H_2}-\mu_*-\mu_{H_2O}\ (19) \color{red} {\Delta}G_{OH^*}={\Delta}G(H_2O(l)+*\rightarrow OH^*+1/2H_2(g)) \color{red} =\mu_{OH^*}+1/2\mu_{H_2}-\mu_*-\mu_{H_2O}\ (20) \color{red} {\Delta}G_{OOH^*}={\Delta}G(2H_2O(g)+*\rightarrow OOH^*+3/2H_2(g)) \color{red} =\mu_{OOH^*}+3/2\mu_{H_2}-\mu_*-2\mu_{H_2O}\ (21) \color{red} \Delta_{H^*}=\Delta G(H^++e^-+*\rightarrow H^*) \color{red} =\mu_{H^*}-1/2\mu_{H_2}-\mu_*
Entropy values of gaseous molecules are taken from the standard tables in Physical Chemistry^[10], while the entropies of adsorbate and adsorption sites are negligible. The zero-point energy for each adsorbate and free molecules can be obtained from the vibration frequency calculation, while the zero-point energy of adsorption sites is negligible.
For each elementary step, the Gibbs reaction free energy Δ G is defined as the difference between free energies of the initial and final states and is given by the expression: \Delta G=\Delta E+\Delta ZPE -T\Delta S+\Delta G_U+\Delta G_{pH} where \Delta E is the reaction energy of reactant and product molecules adsorbed on catalyst surface, obtained from DFT calculations; \Delta ZPE and \Delta ZPE are the change in zero point energies and entropy due to the reaction. The bias effect on the free energy of each initial, intermediate and final state involving an electron in the electrode is taken into account by shifting the energy of the state by \Delta G_U= − neU, where U is the electrode applied potential relative to RHE as mentioned above, e is the elementary charge transferred and n is the number of proton–electron pairs transferred. \Delta G_{pH} is the correction of the H+ free energy and depends on whether the reaction under consideration is a reduction or an oxidation. \Delta G_{pH} = − k_BTln[H+] = pH \times kBTln10, where k_B is the Boltzmann constant and T is the temperature. Hence, the equilibrium potential U_0 for four-electron transfer ORR at pH = 14 was determined to be 0.402 V versus NHE or 1.23 V versus RHE according to the Nernst equation (E= E0 − 0.0591\times pH, U^0_{RHE}=U^0_{NHE}+0.828=1.23 eV, where the reactant and product are at the same energy level.
Given that the high-spin ground state of the oxygen molecule is poorly described in DFT calculations, the free energy of the O₂ molecule was derived according to G_{O_2}(g)=2G_{H_2O}(l)-2G_{H_2}+4*1.23 eV.
The free energy of OH− was derived as G_{OH^−} = G_{H_2O}(l)− G_{H^+}. The free energy for gas phase water is calculated at 0.035 bars because this is the equilibrium pressure in contact with liquid water at 298 K. The free energy of gas phase water at these conditions is equal to the free energy of liquid water.
The reaction free energy of equations (9)–(12) (\Delta G_1, \Delta G_2, \Delta G_3, \Delta G_4) for ORR can be calculated using the following equations: \color{red} \Delta{G_1}=\Delta G_{OOH^*}-4.92\ (24) \color{red} \Delta{G_2}=\Delta G_{O^*}-\Delta G_{OOH^*}\ (25) \color{red} \Delta{G_3}=\Delta G_{OH^*}-\Delta G_{O^*}\ (26) \color{red} \Delta{G_4}=-\Delta G_{OH^*}\ (27)
For ORR, the onset potential is calculated by U_{ORR}^{onset}=-\max\{\Delta G_1,\Delta G_2,\Delta G_3,\Delta G_4\}\ (28) , Nørskov et al. developed a method to determine the overpotentials^[11], \eta^{OER}=1.23-U_{ORR}^{onset}/e\ eV
The reaction free energy of equations (13)–(16) (\Delta G_5, \Delta G_6, \Delta G_7, \Delta G_8) for OER, which are reverse reactions of equations (9)–(12), can be calculated using the following equations: \color{red} \Delta{G_5}=\Delta G_{OH^*}\ (29) \color{red} \Delta{G_6}=\Delta G_{O^*}-\Delta G_{OH^*}\ (30) \color{red} \Delta{G_7}=\Delta G_{OOH^*}-\Delta G_{O^*}\ (31) \color{red} \Delta{G_8}=4.92-\Delta G_{OOH^*}\ (32)
For OER, the onset potential is calculated by U_{OER}^{onset}=\max\{\Delta G_5,\Delta G_6,\Delta G_7,\Delta G_8\} , Nørskov et al. developed a method to determine the overpotentials^[11], \eta^{OER}=U_{OER}^{onset}/e-1.23\ eV . An ideal catalyst should be able to facilitate water oxidation just above the equilibrium potential, but requires all the four charge transfer steps to have reaction free energies of the same magnitude at zero potential (i.e., 4.92 eV/4 = 1.23 eV).

4.3 An Example for ORR

Hydrogen Peroxide Generation with 100% Faradaic Efficiency on Metal-Free Carbon Black^[12]

4.4 Edge Site

Table 1: Calculated free energies at PBE+D3 level.
Group	E (eV)	ZPE-298.15*S_{vib}(eV)	G (eV)
H₂O(0.035bar)	-14.2367	0.579-0.67^[1]	-14.3277
H₂	-6.7689	0.2679-0.41^[1]	-6.9110
O₂	—	—	-9.9134
OH^-	—	—	-10.8722+0.0592*pH
*	-242.2713	—	-242.2713
OH*	-252.7821	0.3914-0.0719	-252.4626
O*	-247.2320	0.0711-0.0591	-247.2200
OOH*	-257.0118	0.4688-0.1504	-256.6934

G_{O_2}=2*G_{H_2O(l)}-2*G_{H_2}+1.23*4
G_{H^++e^-}=1/2G_{H_2}-RTln10\times pH=1/2G_{H_2}-0.0592*pH
G_{OH^-}=G_{H_2O(l)}-G_{H+}=G_{H_2O(l)}-(1/2G_{H_2}-RTln10\times pH)

4.4.1 4e-ORR and 4e-OER for edge site

{\Delta}G_{OH^*}=G_{OH^*}+1/2G_{H_2}-G_*-G_{H_2O}=-252.4626-0.5*6.9110+242.2713+14.3277=0.6809 eV
{\Delta}G_{O^*}=G_{O^*}+G_{H_2}-G_*-G_{H_2O}=-247.2200-6.9110+242.2713+14.3277=2.468000 eV
{\Delta}G_{OOH^*}=G_{OOH^*}+3/2E_{H_2}-E_*-2E_{H_2O}=-256.6934-1.5*6.9110+242.2713+2*14.3277=3.866800 eV
{\Delta}G_{O_2}=4.92 eV

4.4.2 Over potential

\Delta{G_1}=\Delta G_{OOH^*}-4.92=3.866800-4.92=-1.0532 \Delta{G_2}=\Delta G_{O^*}-\Delta G_{OOH^*}=2.468-3.8668=-1.399 \Delta{G_3}=\Delta G_{OH^*}-\Delta G_{O^*}=0.6809-2.468=-1.7871 \Delta{G_4}=-\Delta G_{OH^*}=-0.6809 \Delta{G_5}=\Delta G_{OH^*}=0.6809 \Delta{G_6}=\Delta G_{O^*}-\Delta G_{OH^*}=1.7871 \Delta{G_7}=\Delta G_{OOH^*}-\Delta G_{O^*}=1.399 \Delta{G_8}=4.92-\Delta G_{OOH^*}=1.0532

For OER, the onset potential is calculated by U_{OER}^{onset}=\max\{\Delta G_5,\Delta G_6,\Delta G_7,\Delta G_8\}=1.7871 \eta_{OER}=U_{OER}^{onset}/e-1.23=0.557
For ORR U_{ORR}^{onset}=-\max\{\Delta G_1,\Delta G_2,\Delta G_3,\Delta G_4\}=0.6809 \eta_{ORR}=1.23-U_{ORR}^{onset}/e=0.549

4.4.3 if U=0.7 V (e=-1)

{\Delta}G={\Delta}E+{\Delta}ZPE-T{\Delta}S+eU+{\Delta}G_{pH}

{\Delta}G_{OH^*}=0.6809-0.7=-0.019
{\Delta}G_{O^*}=2.468-0.7*2=1.068
{\Delta}G_{OOH^*}=3.866800-0.7*3=1.767
{\Delta}G_{OOH^*}=4.92-0.7*4=2.120000

4.4.4 2e-ORR

\Delta G_1=\mu_{OOH^*}-\mu_*-\mu_{O_2}-1/2\mu_{H_2}=-256.6934+242.2713+9.9134+0.5*6.9110=-1.0532
\Delta G_2=-1.4-\Delta G_1=-1.4+1.0532=-0.3468
G_{OOH^*}=4.92+\Delta G_1=4.92-1.0532=3.8668
U_{ORR}^{limit}=-\max\{\Delta G_1,\Delta G_2\}=0.3468
Limit Line: (3.52,0)->(4.22,0.7) ->(4.92,0)
In theory, an ideal catalyst should have a G_{OOH^*} of 4.22 (\pm0.1) eV.

Calculated volcano relation of limiting potential U_L as a function of G_{OOH^*}.[12] — Calculated volcano relation of limiting potential U_L as a function of G_{OOH^*}.^[12]

4.4.4.1 U=0.7 V

G_{OOH^*}=3.8668-0.7=3.1668 G_{O_2}=G_{H_2O_2}=3.52

4.4.5 Another Example for volcano plots^[13]

We use G_{OOH^*} as a descriptor and plot the activity volcano to underline the activities of different oxygen functional groups^[14,15]. The limiting potential, U_L, which can be considered a metric of activity, is defined as the lowest potential at which all the reaction steps are downhill in free energy. The theoretical overpotential is defined as the maximum difference between the limiting poten- tial and equilibrium potential.

Calculated two-electron (solid black) ORR-related volcano plot for the electro-reduction of oxygen to H2O2 displayed with the limiting potential plotted as a function of G_{OOH^*}. The equilibrium potential for the two-electron ORR is shown as the dashed black line.[13] — Calculated two-electron (solid black) ORR-related volcano plot for the electro-reduction of oxygen to H₂O₂ displayed with the limiting potential plotted as a function of G_{OOH^*}. The equilibrium potential for the two-electron ORR is shown as the dashed black line.^[13]

Figure 4b shows the calculated U_L as a function of G_{OOH^*} for the two-electron ORR to H₂O₂ on these materials. The structures located on the right side of the volcano bind OOH* weakly, hence equation (1) is a limiting step. Those located on the left side, however, bind OOH* strongly, thus equation (2) is limiting. As a result, the binding strength of OOH* to the surface ultimately determines the ORR activity. The maxi- mum limiting potential is 0.70 V, representing zero overpotential at the top of the volcano.

Ref

[1]

Nørskov, J. K.; Bligaard, T.; Logadottir, A.; Kitchin, J. R.; Chen, J. G.; Pandelov, S.; Stimming, U. Trends in the Exchange Current for Hydrogen Evolution. J. Electrochem. Soc. 2005, 152, J23.

[2]

Chen, Y.; Yu, G.; Chen, W.; Liu, Y.; Li, G.-D.; Zhu, P.; Tao, Q.; Li, Q.; Liu, J.; Shen, X.; et al. Highly Active, Nonprecious Electrocatalyst Comprising Borophene Subunits for the Hydrogen Evolution Reaction. J. Am. Chem. Soc. 2017, 139, 12370–12373.

[3]

Zhang, Z.; Yang, Y.; Gao, G.; Yakobson, B. I. Two-Dimensional Boron Monolayers Mediated by Metal Substrates. Angew. Chem. Int. Ed. 2015, 54, 13022–13026.

[4]

Hinnemann, B.; Moses, P. G.; Bonde, J.; Jørgensen, K. P.; Nielsen, J. H.; Horch, S.; Chorkendorff, I.; Nørskov, J. K. Biomimetic Hydrogen Evolution: MoS _2 Nanoparticles as Catalyst for Hydrogen Evolution. J. Am. Chem. Soc. 2005, 127, 5308–5309.

[5]

Yang, Q.; Xu, W.; Gong, S.; Zheng, G.; Tian, Z.; Wen, Y.; Peng, L.; Zhang, L.; Lu, Z.; Chen, L. Atomically Dispersed Lewis Acid Sites Boost 2-Electron Oxygen Reduction Activity of Carbon-Based Catalysts. Nat. Commun. 2020, 11, 5478.

[6]

Xu, H.; Cheng, D.; Cao, D.; Zeng, X. C. A Universal Principle for a Rational Design of Single-Atom Electrocatalysts. Nat. Catal. 2018, 1, 339–348.

[7]

Li, M.; Zhang, L.; Xu, Q.; Niu, J.; Xia, Z. N-Doped Graphene as Catalysts for Oxygen Reduction and Oxygen Evolution Reactions: Theoretical Considerations. J. Catal. 2014, 314, 66–72.

[8]

Nørskov, J. K.; Rossmeisl, J.; Logadottir, A.; Lindqvist, L.; Kitchin, J. R.; Bligaard, T.; Jónsson, H. Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode. J. Phys. Chem. B 2004, 108, 17886–17892.

[9]

Desai, S. K.; Neurock, M. First-Principles Study of the Role of Solvent in the Dissociation of Water over a Pt-Ru Alloy. Phys. Rev. B 2003, 68, 075420.

[10]

Atkins, P.; de Paula, J. Physical Chemistry. Physical chemistry; Oxford University Press: Oxford, 2010.

[11]

Man, I. C.; Su, H.-Y.; Calle-Vallejo, F.; Hansen, H. A.; Martínez, J. I.; Inoglu, N. G.; Kitchin, J.; Jaramillo, T. F.; Nørskov, J. K.; Rossmeisl, J. Universality in Oxygen Evolution Electrocatalysis on Oxide Surfaces. ChemCatChem 2011, 3, 1159–1165.

[12]

Wang, Z.; Li, Q.-K.; Zhang, C.; Cheng, Z.; Chen, W.; McHugh, E. A.; Carter, R. A.; Yakobson, B. I.; Tour, J. M. Hydrogen Peroxide Generation with 100% Faradaic Efficiency on Metal-Free Carbon Black. ACS Catal, 2021, 11, 2454–2459.

[13]

Lu, Z.; Chen, G.; Siahrostami, S.; Chen, Z.; Liu, K.; Xie, J.; Liao, L.; Wu, T.; Lin, D.; Liu, Y.; et al. High-Efficiency Oxygen Reduction to Hydrogen Peroxide Catalysed by Oxidized Carbon Materials. Nat. Catal. 2018, 1, 156–162.