1 2D elastic constants
1.1 Voigt notation for 2D square, rectangular, or hexagonal lattices
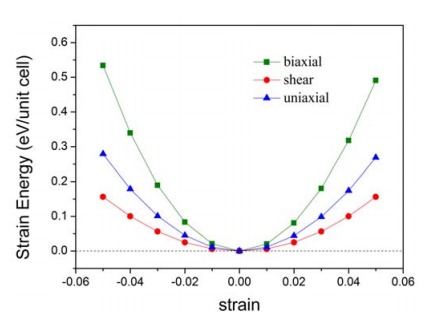
[1,2] As we fix the supercell during all of the MD simulations, it is necessary to assess the effect of lattice distortion on structural stability. To guarantee the positive-definiteness of strain energy following lattice distortion, the linear elastic constants of a stable crystal has to obey the Born–Huang criteria[3]. We calculate the change of energy due to the in-plane strain to determine the mechanical stability of penta-graphene. For a 2D sheet, using the standard Voigt notation[4], i.e., 1-xx, 2-yy, and 6-xy, the elastic strain energy per unit area can be expressed as U(\varepsilon)=\frac{1}{2}C_{11}\varepsilon_{xx}^2+\frac{1}{2}C_{22}\varepsilon_{yy}^2+C_{12}\varepsilon_{xx}\varepsilon_{yy}+2C_{66}\varepsilon_{xy}^2 where C11, C22, C12, and C66 are components of the elastic modulus tensor, corresponding to second partial derivative of strain energy with respect to strain(If hexagonal structures: C_{11}=C_{22},C_{66}=1/2(C_{11}-C_{12}), If square: only C_{11}=C_{22})[4]).
For a mechanically stable 2D sheet[4], the elastic constants need to satisfy C11C22 − C122>0 and C66 > 0[3]. Due to the tetragonal symmetry of penta-graphene, we have C11 = C22. Thus, in this case we only need to satisfy C11>|C12| and C66 > 0. Under uniaxial strain, \varepsilon_{yy} = 0, U(\varepsilon)=1/2C_{11}\varepsilon_{xx}^2. Parabolic fitting of the uniaxial strain curve yields C11 = 265 GPa·nm. Under equi-biaxial strain, \varepsilon_{xx}= \varepsilon_{yy}, we have U(\varepsilon)=(C_{11}+C_{12})\varepsilon_{xx}^2. So Young’s modulus, which can be derived from the elastic constants by Y_{a}=(C_{11}*C_{22}-C_{12}^2)/C_{22},Y_{b}=(C_{11}*C_{22}-C_{12}^2)/C_{11}
- Poisson’s ratio \nu_{a}=C_{12}/C_{22}, \nu_{b}=C_{12}/C_{11}, while Poisson’s ratio \nu the ratio of the transverse strain to the axial strain, namely, \nu=-\varepsilon_{trans}/\varepsilon_{axial} So To check Poisson ration with vasp.impi.fixcell.
1.2 Formula for Orthorhombic systems[5,6]
\begin{pmatrix} \boldsymbol{a_1'} & \boldsymbol{a_2'} & \boldsymbol{a_3'} \end{pmatrix}=\begin{pmatrix} \boldsymbol{a_1} & \boldsymbol{a_2} & \boldsymbol{a_3} \end{pmatrix} \cdot (\boldsymbol{I}+\boldsymbol{\varepsilon}) \boldsymbol{\varepsilon}= \begin{pmatrix} e_1 & e_6/2 & e_5/2 \\ e_6/2 & e_2 & e_4/2 \\ e_5/2 & e_4/2 & e_3 \end{pmatrix}
1.2.1 C_{11} and C_{22}
1.2.1.1 C_{11}
e=(\delta,0,0,0,0,0) E(\delta)=E(0)+\frac{1}{2}C_{11}V_0\delta^2+O(\delta^4) \begin{pmatrix} \boldsymbol{a_1'} & \boldsymbol{a_2'} & \boldsymbol{a_3'} \end{pmatrix} =\begin{pmatrix} \boldsymbol{a_1} & \boldsymbol{a_2} & \boldsymbol{a_3} \end{pmatrix} \cdot \begin{pmatrix} 1+\delta & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}=\begin{pmatrix} (1+\delta) \boldsymbol{a_1} & \boldsymbol{a_2} & \boldsymbol{a_3} \end{pmatrix}
1.2.1.2 C_{22}
e=(0, \delta,0,0,0,0) E(\delta)=E(0)+\frac{1}{2}C_{22}V_0\delta^2+O(\delta^4) \begin{pmatrix} \boldsymbol{a_1'} & \boldsymbol{a_2'} & \boldsymbol{a_3'} \end{pmatrix} =\begin{pmatrix} \boldsymbol{a_1} & (1+\delta) \boldsymbol{a_2} & \boldsymbol{a_3} \end{pmatrix}
1.2.2 C_{12}
1.2.2.1 2D
e=(\delta,\delta,0,0,0,0) E(\delta)=E(0)+\frac{1}{2}(C_{11}+C_{22}+2C_{12})V_0\delta^2+O(\delta^4) \begin{pmatrix} \boldsymbol{a_1'} & \boldsymbol{a_2'} & \boldsymbol{a_3'} \end{pmatrix} =\begin{pmatrix} \boldsymbol{a_1} & \boldsymbol{a_2} & \boldsymbol{a_3} \end{pmatrix} \cdot \begin{pmatrix} 1+\delta & 0 & 0 \\ 0 & 1+\delta & 0 \\ 0 & 0 & 1 \end{pmatrix}=\begin{pmatrix} (1+\delta) \boldsymbol{a_1} & (1+\delta) \boldsymbol{a_2} & \boldsymbol{a_3} \end{pmatrix}
1.2.2.2 3D
u=[1-\delta^2]^{-1/3} e=(u(1+\delta)-1,u(1-\delta)-1,u-1,0,0,0) E(\delta)=E(0)+\frac{1}{2}(C_{11}+C_{22}+2C_{12})V_0\delta^2+O(\delta^4) \begin{pmatrix} \boldsymbol{a_1'} & \boldsymbol{a_2'} & \boldsymbol{a_3'} \end{pmatrix} =\begin{pmatrix} \boldsymbol{a_1} & \boldsymbol{a_2} & \boldsymbol{a_3} \end{pmatrix} \cdot \begin{pmatrix} u(1+\delta) & 0 & 0 \\ 0 & u(1-\delta) & 0 \\ 0 & 0 & u \end{pmatrix}=\begin{pmatrix} u(1+\delta) \boldsymbol{a_1} & u(1-\delta) \boldsymbol{a_2} & u\boldsymbol{a_3} \end{pmatrix}
1.2.3 C_{66}
e=(0,0,0,0,0,\delta) E(\delta)=E(0)+\frac{1}{2}C_{66}V_0\delta^2+O(\delta^4) \begin{pmatrix} \boldsymbol{a_1'} & \boldsymbol{a_2'} & \boldsymbol{a_3'} \end{pmatrix} =\begin{pmatrix} \boldsymbol{a_1} & \boldsymbol{a_2} & \boldsymbol{a_3} \end{pmatrix} \cdot \begin{pmatrix} 1 & \delta/2 & 0 \\ \delta/2 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}=\begin{pmatrix} \boldsymbol{a_1}+\delta/2*\boldsymbol{a_2} & \boldsymbol{a_2}+\delta/2*\boldsymbol{a_1} & \boldsymbol{a_3} \end{pmatrix}
- If set \delta'=\delta/2, then E(\delta)=E(0)+2C_{66}V_0\delta'^2+O(\delta'^4)
1.3 Procedures for 2D square, rectangular lattice
- Hexagonal lattice can be converted to rectangular lattice
1.3.1 Main
- Typically: -0.02\leq \varepsilon \leq 0.02
- S_{cell}=a_{11}*a_{22}\times 10^{-20}\ m^2
- E^s=\frac{U}{S_{cell}}*1.6\times 10^{-19} J/m2
- \Delta E^s=A\varepsilon^2 J/m2
- So U=(E^s_{\varepsilon=0}+A\varepsilon^2)*\frac{S_{cell}}{1.6\times 10^{-19}} J/m2
- Fitting the total energy U vs. \varepsilon using U=A'*\varepsilon**2+B\varepsilon+C
- A=\frac{16}{a_{11}*a_{22}}A'
1.3.2 Uniaxial Strain along x
- Calculate the strain energy per area (E_s) with lateral lattice constant fixed, so that
- \varepsilon_{yy}=0, \Delta E^s=\frac{1}{2}C_{11}\varepsilon_{xx}^2 (C_{11}=\frac{\partial^2 E^s}{\partial\varepsilon_x^2})
- so that C_{11}=2*A_{xx}=\frac{32}{a_{11}*a_{22}}*A'_{xx} J/m2 (1 J/m2 =1 GPa\cdotnm)
1.3.3 Uniaxial Strain along y
- Similarly, \Delta E^s=\frac{1}{2}C_{22}\varepsilon_{yy}^2
- so that, C_{22}=2*A_{yy}=\frac{32}{a_{11}*a_{22}}*A'_{yy} GPa\cdotnm
1.3.4 Biaxial Strain
- \Delta E^s=(\frac{1}{2}C_{11}+\frac{1}{2}C_{22}+C_{12})\varepsilon_{xx}^2
- so that, C_{12}=A_{bi}-\frac{1}{2}C_{11}-\frac{1}{2}C_{22} =\frac{16}{a_{11}*a_{22}}*A'_{bi}-\frac{1}{2}C_{11}-\frac{1}{2}C_{22}
1.3.5 Shear Strain
- \Delta E^s=2C_{66}\varepsilon_{xy}^2
- So that C_{66}=2*A_{xy}=\frac{8}{a_{11}*a_{22}}*A'_{xy}
1.3.6 Other tips
- For 2D square system: C_{11}=C_{22}
- For 2D hexagonal system: C_{11}=C_{22}, C_{66}=1/2(C_{11}-C_{12})
- Young’s modulus: Y_{a}=(C_{11}*C_{22}-C_{12}^2)/C_{22} , Y_{b}=(C_{11}*C_{22}-C_{12}^2)/C_{11}
- Poisson’s ratio: \nu_{a}=C_{12}/C_{22}, \nu_{b}=C_{12}/C_{11}
- layer modulus[4]: \gamma=1/4(C_{11}+C_{22}+2C_{12})
2 Graphene
Table. Elastic constants (GPa) for graphene. Rec and hex stand for rectangular and hexagonal lattice.
| Graphene | C_{11} | C_{22} | C_{12} | 1/2(C_{11}-C_{12}) | C_{66} |
|---|---|---|---|---|---|
| This work | 352.62 (Rec) | 352.25 (Rec) | 61.43 (Rec) | 145.59 (Rec) | 149.56 (Hex. +Relaxtion) |
| Ref.[2] | 342.93 | 342.93 | 62.23 | 140.35 | — |
3 persistence length
[7] another important measure of stiffness is so-called persistence length[31] lp (a correlation length for the direction of a tube exposed to equilibrium fluctuations at temperature T). Its magnitude is proportional to the tube stiffness, l_{p}=\pi Cd^3/8k_BT, and amounts to fraction of a millimeter at room temperature for the typical nanometer diameters.
radial breathing mode (RBM) frequency
f_{RBM}=(1/\pi{c}{d})/[(C/(1-\nu^2)\rho_s)^{1/2}] where \rho_s is the mass density of the sheet per unit area. (The speed of light c is to convert to spectroscopic cm-1 units.), d:nanotube diameters, \nu:Poisson ratio,C:in-plane stiffness
4 Bulk modulus
- Yang modulus: \frac{1}{E}=\frac{1}{3G_{\nu}}+\frac{1}{K_{\nu}}
- Bulk modulus G_{\nu} (Voigt notation): 15G_{\nu}=(C{11}+C{22}+C{33})-(C{12}+C{23}+C{31})+3(C{44}+C{55}+C{66})
- Hardness {K_{\nu}} (Voigt notation): 9K_{\nu}=(C{11}+C{22}+C{33})+2(C{12}+C{23}+C{31})
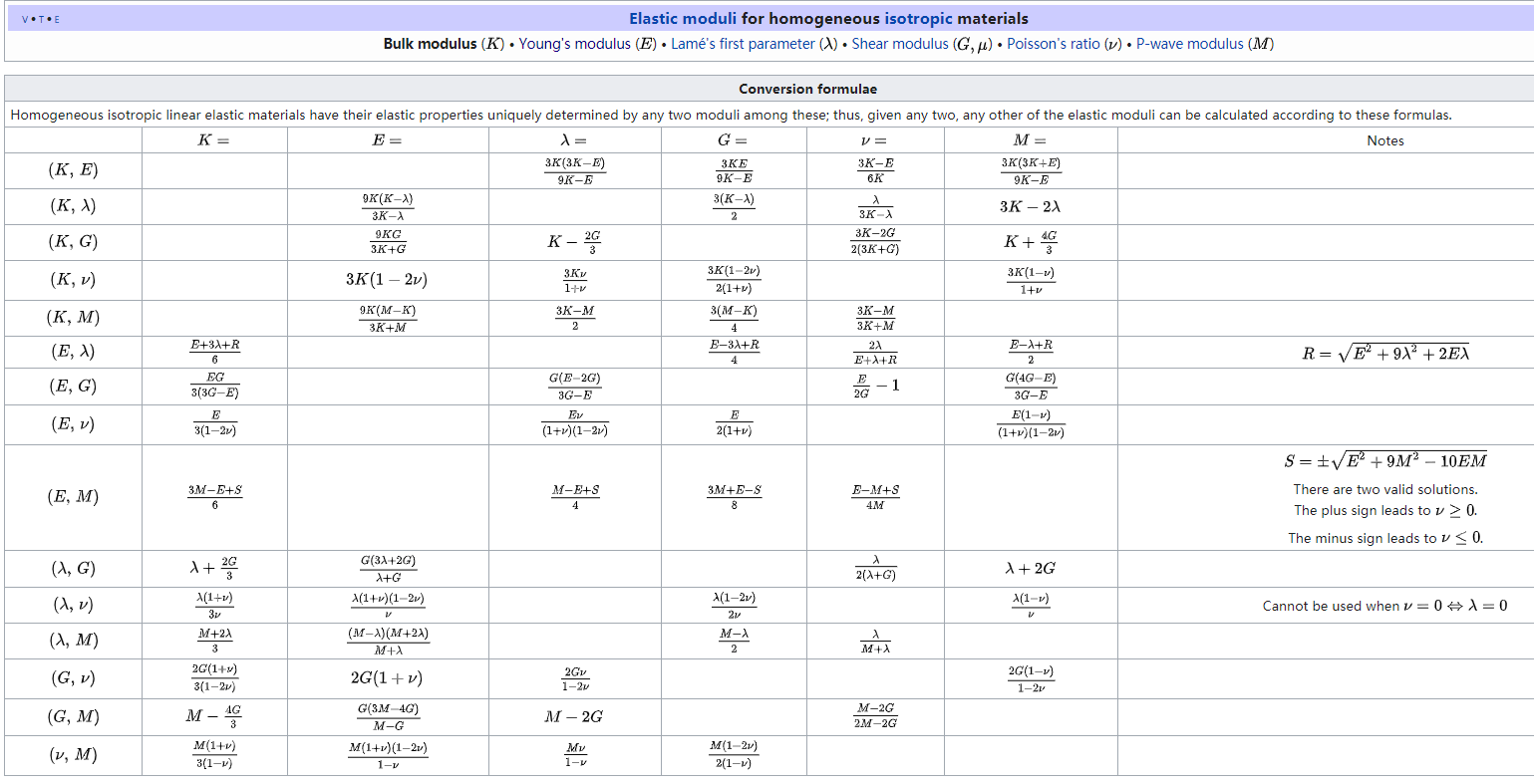
5 From wikipedia