1 Effective mass

m_e^*=\hbar[\frac{\partial^2E(k)}{\partial k^2}]^{-1}

2 1D Mobility^[1,2]

An expression for the mobility in 1D systems is \mu_{1D}=\sqrt{\frac{2}{\pi}}\frac{e\hbar^2 C^{1D}}{\sqrt{k_B T} (m_e^*)^{3/2} E_l^2} which should be relevant for BP ribbons. The narrower the ribbon, the smaller is its effective elastic modulus.

3 2D Mobility^[1]

In 2D the carrier mobility is given by the expression \mu^{2D}=\frac{e\hbar^3 C^{2D}}{k_B T m_c^* m_d (E_l^i)^2} where m_c^* is the effective mass in the transport direction and m_d is the average effective mass determined by m_d=\sqrt{m_x^*m_y^*} . The term E_l represents the deformation potential constant of the valence-band minimum for hole or conduction-band maximum for electron along the transport direction, defined by E_l^i(VBM/CBM)=\frac{\Delta (E(VBM/CBM)-E(vac))}{\Delta l/l_0}

Here {\Delta}V_i is the energy change of the ith band under proper cell compression and dilatation (calculated using a step of 0.5%), l_0 is the lattice constant in the transport direction and {\Delta}l is the deformation of l_0. The elastic modulus C^{2D} of the longitudinal strain in the propagation directions (both x and y) of the longitudinal acoustic wave is derived from (E_l-E_0)/S_0=\frac{ C^{2D}}{2}(\Delta l/l_0)^2 \Rightarrow E_l=E_0+\frac{S_0 C^{2D}}{2}(\Delta l/l_0)^2

,where E is the total energy and S_0 is the lattice volume at equilibrium for a 2D system. All structural properties in the calculation of carrier mobilities were obtained from optB88-vdW and properties related to the electronic structure were computed with the HSE06 functional. The temperature used for the mobility calculations was 300 K.

E_{deform}=slope

4 Unit Conversion

\mu^{2D}=\frac{e\hbar^3 C^{2D}}{k_B T m_c^* m_d (E_l^i)^2}

=\frac{\sout{1.602\times10^{-19}CV}/V*(1.054571817\times10^{-34})^3J^3s^3 C^{2D}N/m}{1.380649\times10^{-23}J/\sout{K}*300\sout{K}*m_c^ * m_d * (9.10956\times10^{-31})^2 kg^2 (E_l^i)^2*(1.602\times10^{-19}CV)^{\sout2}}

=\frac{(1.054571817\times10^{-34})^3Js^3/V C^{2D}J/m^2}{1.380649\times10^{-23} *300 *m_c^ * m_d * (9.10956\times10^{-31})^2 kg^2 (E_l^i)^2*(1.602\times10^{-19})}

=\frac{(1.054571817\times10^{-34})^3Js^{\sout{3}}/V C^{2D}\sout{J/m^2}}{1.380649\times10^{-23} *300 *m_c^ * m_d * (9.10956\times10^{-31})^2 kg^{\sout{2}} (E_l^i)^2*(1.602\times10^{-19})}

=\frac{2.1104\times10^{-3}C^{2D}}{m_c^ * m_d(E_l^i)^2}J\cdot s/V/kg =\frac{21.104C^{2D}}{m_c^ * m_d(E_l^i)^2} cm^2V^{-1}s^{-1}

where the units for C^{2D}, m_c^*, m_d and E_l^i are N/m, m_0, m_0 and eV, respectively.

• 1J=1CV, 1J=1kg\cdot m^2/s^2

5 Example of B₄C₃ sheet^[3]

5.1 Note

• Usually the realtion between lattice vector a_{i} and reciprocal lattice vector b_{j} is esspresed as a_{i}*b_{j}=2{\pi}{\Delta}_{ij}, however it is esspresed as a_{i}*b_{j}={\Delta}_{ij} in VASP，so the unit of reciprocal lattice vectors in VASP is 2\pi. If you use reciprocal lattice vectors from vasp, please multiply the reciprocal lattice vectors with 2\pi

5.2 Formula for effective mass:

E(k)=E_0+\frac{\hbar^2k^2}{2m*}=A*k^2+Bk+C \frac{\hbar^2}{m^*}=\frac{\partial^2E}{\partial^2k}=2A\Rightarrow\frac{1}{m^*}=\frac{1}{\hbar^2}\frac{\partial^2E}{\partial^2k} * In atomic units, m^*=\frac{1}{2A}

5.2.1 Calculation

1. Optimize cell
2. Band structure calculation, to determine VBM and CBM.
3. Non-SCF calculation with very dense K-points near the VBM/CBM point, to get VB and CB energy surfaces.
4. Use some script to generate files (e.g., eig_bandsurf_024.dat) for the energy surface of VB/CB at every K points,

$ head eig_bandsurf_024.dat
Kx             Ky             Kz             Energy  Kx*Rec         Ky*Rec         Kz*Rec
-0.01500000    -0.01500000    0.00000000     -0.27691100    -0.01163803    -0.02017344    -0.00000006
-0.01350000    -0.01500000    0.00000000     -0.27680900    -0.01047423    -0.02017344    -0.00000006
-0.01200000    -0.01500000    0.00000000     -0.27672800    -0.00931042    -0.02017344    -0.00000006
-0.01050000    -0.01500000    0.00000000     -0.27666400    -0.00814662    -0.02017344    -0.00000006
...

where Kx/Ky/Kz are K points near VBM/CBM，Kx*Rec/Ky*Rec/Kz*Rec are K points multiplied by reciprocal lattice vectors (similar to the conversion from Direct coordinates to Cartesian coordinates), and Energy is the energy for this band at Kx/Ky/Kz.
5. Extract K lines across VBM/CBM point (e.g., \Gamma) along x/y direction with atomic unit convertion:

awk '($1~/0.00000000/){print $6*0.529,$4/27.21}' eig_bandsurf_024.dat >emass_vb_ky_au.dat
awk '($2~/0.00000000/){print $5*0.529,$4/27.21}' eig_bandsurf_024.dat >emass_vb_kx_au.dat
awk '($1~/0.00000000/){print $6*0.529,$4/27.21}' eig_bandsurf_025.dat >emass_cb_ky_au.dat
awk '($2~/0.00000000/){print $5*0.529,$4/27.21}' eig_bandsurf_025.dat >emass_cb_kx_au.dat

• 1 bohr=0.529, 1 Ha= 27.21 eV.

6. Using gnuplot for Parabolic Fitting: y=col(2) vs. x=col(1) to get the coefficient A. According to m^*=\frac{1}{2A}, m_h^*(x)=1.6415, m_h^*(y)=0.4427, m_e^*(x)=2.4546, m_e^*(y)=0.2908 in unit of the mass of free electron.

5.3 Deformation Energy and Elastic Modulus (2D)

5.3.1 Calculation C_x^{2D}

1. Change lattice parameter a (\varepsilon=98\%\sim102\%)
2. Optimize the Cell and atomic positions with lattice vector \bold{a} and \bold{c} fixed while \bold{b} released considering Poisson Effect.
   
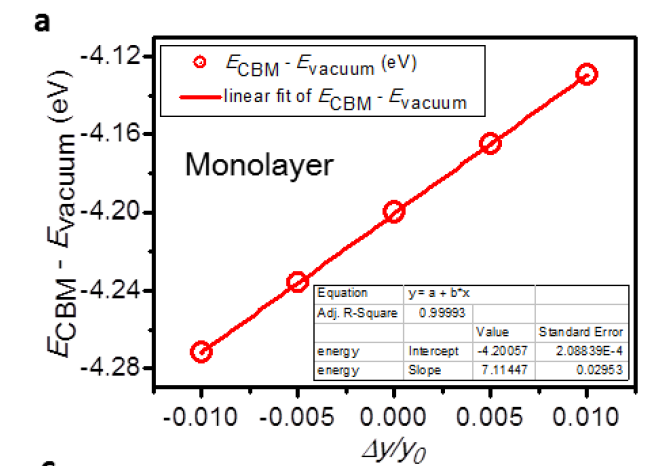
3. Performe a SCF calculation with LVHAR=.TRUE., get total energy, Vaccum level, VBM and CBM for each step.
4. Linear fitting on y=E_{VBM}-E_{vac} vs. x=\varepsilon to get slope=E_{deform}^h, and y=E_{CBM}-E_{vac} vs. x=\varepsilon to get slope=E_{deform}^e
5. Parabolic Fitting on y=energy vs. x=\varepsilon to get C_x^{2D}=\frac{2A}{S_0}eV/\AA²=\frac{16.02*2A}{S_0}N/m..
6. An example,
   

• \mu_x^{2D}(e)=\frac{21.104C_x^{2D}}{m_c^ * m_d(E_l^x)^2} cm²V^-1s^-1 =21.104*(16.02*2*280.56/8.09825/4.6718746924056926)/2.4546*\sqrt(2.4546*0.2908)/2.26^2=337.9 cm²V^-1s^-1

Ref