:D 获取中...

1 Determine U and J value

  • U and J are screened Coulomb and exchange parameters
  • The exchange J (typically of order ~1 eV[1]), though not as strong as that of U (about one-tenth of U in magnitude), may also play an important role on band gaps[1].

2 Calculating the Hubbard U by linear-response method

2.1 FROM MIT

Tuesday, May 31, 2011

If you you think you might be interested in carrying out DFT+U calculations on a system, this tutorial is tailor made for you.  

2.1.1 Background

Recall, the DFT+U functional, as implemented in [Quantum-ESPRESSO][2] corresponds to an additional term of the form: E_U=\frac{U}{2}\sum\limits_{I,\sigma}Tr[\bold{n}^{i\sigma}(1-\bold{n}^{i\sigma})] The use of this functional form is particularly motivated by systems consisting of transition-metals with localized electrons (i.e. d or f) that standard DFT struggles to treat accurately.  

Before embarking on production level simulations, one of the first things you should always do is to calculate the value of U for your system. In our linear-response U approach[2], the response function that we calculate is: \chi=\frac{\partial{n}{\partial\alpha} with a matrix of response functions in the case of multiple sites but a single value for single site systems. In order to obtain U, we invert the self-consistent response function and subtract out the bare, non-interacting response[2]: U=\chi_0^{-1}-\chi^{-1} Today we will only address the single site example of MnO[3], but a future tutorial will expand the calculation to more manifolds.

2.1.2 Instruction

The determination of the linear-response U is simple and costs little more than a standard single point energy calculation, which is something you have likely already carried out for the system of interest.  Using the scripts provided below, we can easily calculate the linear response U for the sextet ground state of the diatomic molecule MnO.

We obtain the bare and self-consistent response functions from linear regression of the relationship between the occupations that result from a range of rigid potential shifts, alpha:

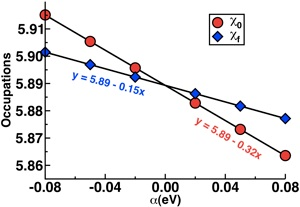
For sextet MnO, the bare and self-consistent slopes are -0.32 and -0.15, respectively, giving U0 = 3.47 eV.

We determine the linear-response U as follows:

  1. Obtain single point energy at zero alpha and store density.

  2. Starting from 1, obtain new single point energy at several values ofnon-zero alpha (e.g. -0.08 to 0.08) with tight convergence criteria.

  3. Collect occupations from first iteration of 2 for bare response and last iteration of 2 for self-consistent response.

  4. Calculate response functions from linear regression of 3** and invert to obtain U.

The additional single points in step 2 should each take less than half of the time of the original single point in step 1 because the addition of alpha is only a small perturbation. (Note: The key here is to ensure that you can copy over the starting zero-alpha density each time for each non-zero alpha calculation). One approach for the file copying step is implemented in the main script, jobrun.py, and clarified in the variables file, variables.py.  The linear regression is carried out after completion of the SCF runs inlinregress.py and the results are written to the file ucalc.dat.  

In addition to the standard linear-response U0, the self-consistent extension,Uscf[3], can be determined with these scripts.  This approach is carried out automatically by setting a range of values of Uin (e.g. 0.5-3.0 eV in 0.5 eV increments) in the file variables.py.  

The linear-response and self-consistent U values are essentially identical for sextet MnO. The self-consistent U is determined from the extrapolation ofUout calculated over a range of Uin where the relationship is linear[2].  Larger differences between the self-consistent and linear-response U values can be much larger, especially where the electronic structure between DFT and DFT+U differs significantly. We have also studied systems from a few to hundreds of atoms in size with self-consistent DFT+U, and I encourage you to read about the research and the relevant publications.

2.1.3 Summary

The tutorial files, provided also as a zipped archive here, are:

  • jobrun.py— skeleton script generates input files and runs jobs. 

  • variables.py — you should change these job and cluster variables!  

  • libraries.py — dictionary of parameters that should not be changed.

  • linregress.py — calculates U0 and Uscf from results of jobrun.py.

  • other files — pseudopotentials, coordinates for MnO, a readme file, and an example job script for SGE queues.

I hope that this tutorial has helped you to better understand how to calculate the linear-response and self-consistent Hubbard U for single-site transition metal complexes.  Please [email me] if you have any additional questions not answered here!

2.2 Calculate U for LSDA+U (VASP wiki)

In this exercise you will calculate the U parameter for the LSDA+U treatment of Ni d-electrons in NiO using the linear response ansatz of Cococcioni et al..[2]

2.2.1 POSCAR

For this calculation we will use a 2×2×2 supercell of AFM-II NiO:

AFM  NiO
   4.03500000 
 2.0000000000   1.0000000000   1.0000000000 
 1.0000000000   2.0000000000   1.0000000000 
 1.0000000000   1.0000000000   2.0000000000 
  1 15   16 
Direct
 0.0000000000   0.0000000000   0.0000000000 
 0.2500000000   0.2500000000   0.2500000000 
 0.0000000000   0.0000000000   0.5000000000 
 0.2500000000   0.2500000000   0.7500000000 
 0.0000000000   0.5000000000   0.0000000000 
 0.2500000000   0.7500000000   0.2500000000 
 0.0000000000   0.5000000000   0.5000000000 
 0.2500000000   0.7500000000   0.7500000000 
 0.5000000000   0.0000000000   0.0000000000 
 0.7500000000   0.2500000000   0.2500000000 
 0.5000000000   0.0000000000   0.5000000000 
 0.7500000000   0.2500000000   0.7500000000 
 0.5000000000   0.5000000000   0.0000000000 
 0.7500000000   0.7500000000   0.2500000000 
 0.5000000000   0.5000000000   0.5000000000 
 0.7500000000   0.7500000000   0.7500000000 
 0.1250000000   0.1250000000   0.1250000000 
 0.3750000000   0.3750000000   0.3750000000 
 0.1250000000   0.1250000000   0.6250000000 
 0.3750000000   0.3750000000   0.8750000000 
 0.1250000000   0.6250000000   0.1250000000 
 0.3750000000   0.8750000000   0.3750000000 
 0.1250000000   0.6250000000   0.6250000000 
 0.3750000000   0.8750000000   0.8750000000 
 0.6250000000   0.1250000000   0.1250000000 
 0.8750000000   0.3750000000   0.3750000000 
 0.6250000000   0.1250000000   0.6250000000 
 0.8750000000   0.3750000000   0.8750000000 
 0.6250000000   0.6250000000   0.1250000000 
 0.8750000000   0.8750000000   0.3750000000 
 0.6250000000   0.6250000000   0.6250000000 
 0.8750000000   0.8750000000   0.8750000000

Atoms 1-16 are Ni and atoms 17-32 are O.

Note that the Ni atoms are split into two groups: atom 1, and atom 2-15. This trick breaks the symmetry of the Ni sub-lattice and allows us to treat atom 1 differently from atom 2-15. Our POTCAR file has to reflect the fact that we now formally have 3 "species" (2 ×Ni + 1×O), i.e., we concatenate two Ni POTCAR files and one O POTCAR file:

cat Ni/POTCAR Ni/POTCAR O/POTCAR > POTCAR

To check whether you have a suitable POTCAR type:

grep TITEL POTCAR

This should yield something like:

TITEL = PAW Ni 02Aug2007
TITEL = PAW Ni 02Aug2007
TITEL = PAW O 22Mar2012

i.e., two Ni entries followed by one O entry.

2.3 KPOINTS

Gamma only
0
Monkhorst
1 1 1
0 0 0

2.4 The DFT groudstate

We will calculate the DFT groundstate of our NiO system with the following INCAR:

SYSTEM       = NiO AFM 
PREC         = A
EDIFF        = 1E-6
ISMEAR       = 0
SIGMA        = 0.2
ISPIN        = 2
MAGMOM       = 1.0 -1.0  1.0 -1.0  1.0 \
              -1.0  1.0 -1.0  1.0 -1.0 \
               1.0 -1.0  1.0 -1.0  1.0 \
              -1.0  1.0 -1.0  1.0 -1.0 \
            16*0.0

LORBIT       = 11
LMAXMIX      = 4

Instrumental here is that we correctly specify the initial magnetic moments (by means of MAGMOM). The setting above is consistent with the AFM-II magnetic structure: alternating ferromagnetic Ni (111)-layers.

Secondly we set LORBIT=11: at the end of the OUTCAR file VASP will write the number of (d-) electrons per site. This information we will need to compute the U-parameter.

Last but not least, we set LMAXMIX=4: this is needed to be able to perform non-selfconsistent (ICHARG=11) LSDA+U calculations (LDAUTYPE=3) in the following. For this reason we will keep a copy of the CHGCAR file (and the WAVECAR file as well):

cp CHGCAR CHGCAR.0
cp WAVECAR WAVECAR.0

The information most relevant to the task at hand you will find near the end of the OUTCARfile:

total charge

 total charge

# of ion       s       p       d       tot
------------------------------------------
    1        0.342   0.490   8.438   9.269
    2        0.342   0.490   8.438   9.269
    3        0.342   0.490   8.438   9.270
    4        0.342   0.490   8.438   9.269
    5        0.342   0.490   8.438   9.269
    6        0.342   0.490   8.438   9.269
    7        0.342   0.490   8.438   9.269
    8        0.342   0.490   8.438   9.269
    9        0.342   0.490   8.438   9.269
   10        0.342   0.490   8.438   9.269
   11        0.342   0.490   8.438   9.269
   12        0.342   0.490   8.438   9.269
   13        0.342   0.490   8.438   9.269
   14        0.342   0.490   8.438   9.270
   15        0.342   0.490   8.438   9.269
   16        0.342   0.490   8.438   9.269
   17        1.564   3.455   0.000   5.019
   18        1.564   3.455   0.000   5.019
   19        1.564   3.455   0.000   5.019
   20        1.564   3.455   0.000   5.019
   21        1.564   3.455   0.000   5.019
   22        1.564   3.455   0.000   5.019
   23        1.564   3.455   0.000   5.019
   24        1.564   3.455   0.000   5.019
   25        1.564   3.455   0.000   5.019
   26        1.564   3.455   0.000   5.019
   27        1.564   3.455   0.000   5.019
   28        1.564   3.455   0.000   5.019
   29        1.564   3.455   0.000   5.019
   30        1.564   3.455   0.000   5.019
   31        1.564   3.455   0.000   5.019
   32        1.564   3.455   0.000   5.019
--------------------------------------------------
tot         30.489  63.111 135.011 228.611

This shows that in the DFT grounstate 8.438 d-electrons are attributed to atomic site 1.

2.5 Non-selfconsistent response

The next step is to calculate the following response function: \chi_{IJ}^0=\frac{\partial N_I^{NSCF}{\partial V_J}

This is the change in the number of d-electrons on site I due to an additional spherical potential acting on the d-manifold on site J. In the following we will assume this response to be zero unless I=J.

To add an additional spherical potential on the site of atom 1 that acts on the d-manifold we specify the following:

LDAU         = .TRUE.
LDAUTYPE     =  3
LDAUL        =  2 -1 -1
LDAUU        =  0.10 0.00 0.00
LDAUJ        =  0.10 0.00 0.00

Note that for LDAUTYPE=3 the LDAUUand LDAUJ tags specify the strength (in eV) of the spherical potential acting on the spin-up and spin-down d-manifolds, respectively.

In the present step we want to calculate the non-selfconsistent response to this additional potential. This is done by reading in the charge density from the previous DFT groundstate calculations and by keeping it fixed during the electronic minimization procedure:

ICHARG= 11

N.B.: be sure to use the charge density of the DFT groundstate calculation:

cp CHGCAR.0 CHGCAR
cp WAVECAR.0 WAVECAR

After running this calculation you will notice that due to the additional potential the number of d-electrons on atom 1 has changed w.r.t. the DFT groundstate (check the OUTCARfile again):

 total charge

# of ion       s       p       d       tot
------------------------------------------
    1        0.342   0.490   8.488   9.319
    2        0.342   0.489   8.432   9.263
    3        0.342   0.490   8.438   9.269
    4        0.342   0.490   8.438   9.269
    5        0.342   0.490   8.438   9.269
    6        0.342   0.490   8.438   9.269
    7        0.342   0.490   8.435   9.266
    8        0.342   0.490   8.438   9.269
    9        0.342   0.490   8.438   9.269
   10        0.342   0.490   8.438   9.269
   11        0.342   0.490   8.435   9.266
   12        0.342   0.490   8.438   9.269
   13        0.342   0.490   8.435   9.266
   14        0.342   0.490   8.438   9.269
   15        0.342   0.490   8.430   9.261
   16        0.342   0.489   8.432   9.263
   17        1.564   3.455   0.000   5.019
   18        1.564   3.455   0.000   5.018
   19        1.564   3.454   0.000   5.018
   20        1.564   3.454   0.000   5.018
   21        1.564   3.454   0.000   5.018
   22        1.564   3.454   0.000   5.018
   23        1.564   3.454   0.000   5.018
   24        1.564   3.454   0.000   5.018
   25        1.564   3.454   0.000   5.018
   26        1.564   3.454   0.000   5.018
   27        1.564   3.454   0.000   5.018
   28        1.564   3.454   0.000   5.018
   29        1.564   3.454   0.000   5.018
   30        1.564   3.454   0.000   5.018
   31        1.564   3.455   0.000   5.018
   32        1.564   3.455   0.000   5.019
--------------------------------------------------
tot         30.488  63.101 135.027 228.617

The change in the number of d-electrons on atomic site 1 is found to be: \Delta{N}_1^{NSCF}=4.488−4.438 = 0.050 and hence \chi_{11}^0=\frac{0.050}{0.1}=0.5\ eV^{-1}

2.6 Selfconsistent response

The selfconsistent reponse function: \chi_{IJ}^0=\frac{\partial N_I^{SCF}}{\partial V_J}

is computed in a similar manner:

LDAU         = .TRUE.
LDAUTYPE     =  3
LDAUL        =  2 -1 -1
LDAUU        =  0.10 0.00 0.00
LDAUJ        =  0.10 0.00 0.00

N.B.I: The only difference between this calculation and the previous calculation of the non-selfconsistent response is that now we do not set ICHARG=11, i.e, now the charge density may change.

N.B.II: To speed things up it is a good idea to restart this calculation from the WAVECAR file of the previous non-selfconsistent response calculation.

After this calculation has finished you should again inspect the number of d-electrons on atomic site 1:

 total charge

# of ion       s       p       d       tot
------------------------------------------
    1        0.341   0.488   8.452   9.281
    2        0.342   0.490   8.438   9.269
    3        0.342   0.490   8.438   9.269
    4        0.342   0.490   8.438   9.269
    5        0.342   0.490   8.438   9.269
    6        0.342   0.490   8.438   9.269
    7        0.342   0.490   8.438   9.269
    8        0.342   0.490   8.438   9.269
    9        0.342   0.490   8.438   9.269
   10        0.342   0.490   8.438   9.269
   11        0.342   0.490   8.438   9.269
   12        0.342   0.490   8.438   9.269
   13        0.342   0.490   8.438   9.269
   14        0.342   0.490   8.438   9.269
   15        0.342   0.490   8.438   9.269
   16        0.342   0.490   8.438   9.269
   17        1.564   3.455   0.000   5.019
   18        1.564   3.455   0.000   5.019
   19        1.564   3.455   0.000   5.018
   20        1.564   3.455   0.000   5.019
   21        1.564   3.455   0.000   5.018
   22        1.564   3.455   0.000   5.019
   23        1.564   3.455   0.000   5.019
   24        1.564   3.455   0.000   5.018
   25        1.564   3.455   0.000   5.018
   26        1.564   3.455   0.000   5.019
   27        1.564   3.455   0.000   5.019
   28        1.564   3.455   0.000   5.018
   29        1.564   3.455   0.000   5.019
   30        1.564   3.455   0.000   5.018
   31        1.564   3.455   0.000   5.019
   32        1.564   3.455   0.000   5.019
--------------------------------------------------
tot         30.488  63.107 135.022 228.617

The change in the number of d-electrons on atomic site 1 is found to be: \Delta{N}_1^{NSCF}=4.452 − 4.438 = 0.012 and hence \chi_{11}^0=\frac{0.012}{0.1}=0.12\ eV^{-1}

2.7 The final result

After we have computed both the non-selfconsistent as well as the selfconsistent response functions, the U parameter for the LSDA+U treatment of Ni d-electrons in NiO is found from:

U=\chi^{-1}-\chi_{0}^{-1}\approx (\frac{\partial N_{I}^{SCF}}{\partial V_{I}})^{-1}- (\frac{\partial N_{I}^{NSCF}}{\partial V_{I}})^{-1} =\frac{1}{0.12}-\frac {1}{0.5}=6.33\ eV

To get a more accurate result one should repeat the previous calculations for a series of different additional potentials (for instance LDAUU=LDAUJ= -0.2, -0.15, -0.10, -0.05, 0.05, 0.10 ,0.15, and 0.20 eV). All necessary steps are scripted in doall.sh in the tgz-file below.

The relevant response functions are then easily found from a linear fit of the number of d-electrons on atomic site 1 as a function of the additional potential V:

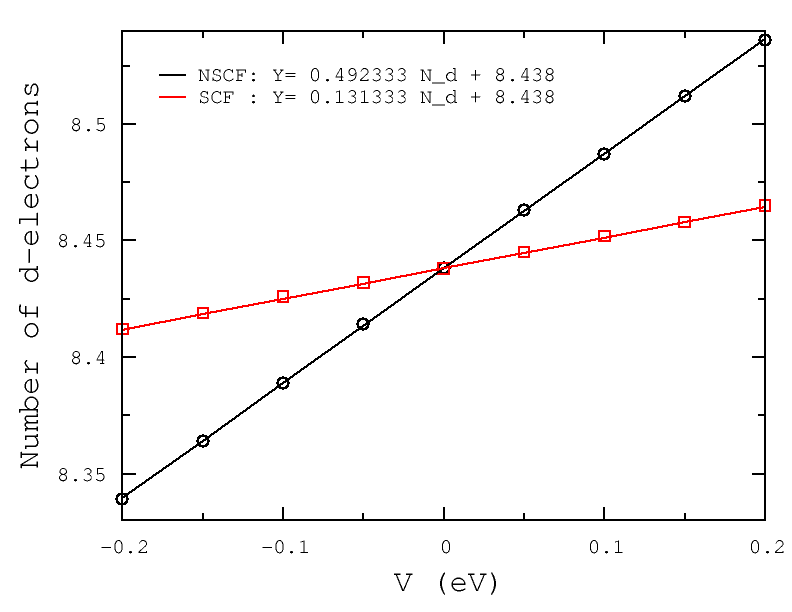
From the above we then have: U=\chi^{-1}-\chi_{0}^{-1}\approx (\frac{\partial N_{I}^{SCF}}{\partial V_{I}})^{-1}- (\frac{\partial N_{I}^{NSCF}}{\partial V_{I}})^{-1} =\frac{1}{0.13133}-\frac {1}{0.49233}=5.58\ eV

3 some U and J values

  • U values seem to depend on the oxidation states and the functional used.
  • U-J=0.8 for Co[4]
  • 5-6 eV for LDA+U and 2–3 eV for GGA+U[5]
  • U value must satisfy the criteria of U > 6 eV for LDA calculations and U > 5 eV for GGA calculations to exactly predict the ground state of Ce2Ox.[6]
  • 3d轨道U和J计算如下所示：主要原理是改变d轨道的占据，在自旋极化的前提下计算不同自旋轨道能量的差值提取U和J，U为Coulomb排斥能，J是交换能，U在所有电子中都存在，不管自旋是否相同，J只存在于自旋相同的电子上。[7]
Table: Some U and J values
Species U J U－J(Ueff)
CaCuO3 7.5 0.98 6.5
NiO 8.0 0.95 7.1
CoO 7.8 0.92 6.9
FeO 6.8 0.89 5.9
MnO 6.9 0.86 10.3
VO 6.7 0.81 5.9
TiO 6.6 0.78 5.8

3.1 GGA+U from Materials Project

3.2 Calibration of U values

The U values were obtained by fitting to experimental binary formation enthalpies as described in Wang et al.'s work, which is simple and accurately reproduces phase stabilities. A least squares method of obtaining the correct U value was used, as follows:

  1. For each non-overlapping formation energy reaction considered, we find the region where the formation energy error passes zero. For the V-O system, this includes the following:
    1. 2 V2O3 + O2 → 4 VO2
    2. 4VO2 + O2 → 2 V2O5
  2. For each formation energy region identified, we fit the linear equation \begin{align} \mbox{Error/redox} & = m U + c \end{align} to the final U range. In the case of V, we will have two sets of (m,c).
  3. We find the U value that minimizes the sum of square Error / Redox.
  4. In the case of V, we get a U value of 3.25.

3.3 U values

The full list of U values used is described in the table below. For oxide containing any of the elements, both GGA and GGA+U calculations were performed.

Calibrated U values for Transition Metals
Element System Fitting Reaction Redox Couple Calibrated U (eV) Comments
Co Oxides 6 CoO + O2 → 2 Co3O4 Co2+ → Co2.67+ 3.32
Cr Oxides 2/3 Cr2O3 + O2 → 4/3 CrO3 Cr3+ → Cr6+ 3.7
Fe Oxides 6 FeO + O2 → 2 Fe3O4
4 Fe3O4 + O2 → 6 Fe2O3		 Fe2+ → Fe2.67+
Fe2.67+ → Fe3+		 5.3
Mn Oxides 6 MnO + O2 → 2 Mn3O4
Mn3O4 + O2 → 3 MnO2		 Mn2+ → Mn2.67+
Mn2.67+ → Mn4+		 3.9 Mn2O3 was explicitly excluded from calibration set
due to the large number of atoms in its unit cell.
Mo Oxides 2 MoO2 + O2 → 2 MoO3 Mo4+ → Mo6+ 4.38
Ni Oxides Li2O + NiO + O2 → LiNiO2 Ni2+ → Ni3+ 6.2 Binary formation energies are not readily available for the Ni.
The Ni U calibration was performed using a ternary oxide formation energy.[5]
V Oxides 2 V2O3 + O2 → 4 VO2
4 VO2 + O2 → 2 V2O5		 V3+ → V4+
V4+ → V5+		 3.25 VO was explicitly excluded from calibration set
due to its known metallic nature.
W Oxides 2 WO2 + O2 → 2 WO3 W4+ → W6+ 6.2

3.4 Caveats

The U values are calibrated for phase stability analyses, and should be used with care if applied to obtain other properties such as band structures. Also, the U values depend on the pseudopotential used. A discussion of the pseudopotentials used in the Materials Project can be found here.

References

[1]
Anisimov, V. I.; Aryasetiawan, F.; Lichtenstein, A. I. First-Principles Calculations of the Electronic Structure and Spectra of Strongly Correlated Systems: The LDA+U Method. J. Phys. Condens. Matter. 1997, 9, 767–808.
[2]
Cococcioni, M.; de Gironcoli, S. Linear Response Approach to the Calculation of the Effective Interaction Parameters in theLDA\mathplus{}{}U{}{m}ethod. Phys. Rev. B 2005, 71, 035105.
[3]
Kulik, H. J.; Cococcioni, M.; Scherlis, D. A.; Marzari, N. Density Functional Theory in Transition-Metal Chemistry: A Self-Consistent Hubbard $U$ Approach. Phys. Rev. Lett. 2006, 97, 103001.
[4]
Zhou, W.; Sunarso, J.; Zhao, M.; Liang, F.; Klande, T.; Feldhoff, A. A Highly Active Perovskite Electrode for the Oxygen Reduction Reaction Below 600. Angew. Chem. Int. Ed. 2013, 52, 14036–14040.
[5]
Loschen, C.; Carrasco, J.; Neyman, K. M.; Illas, F. First-Principles $\Mathrm{}LDA{}+\mathrm{}U{}$ and $\Mathrm{}GGA{}+\mathrm{}U{}$ Study of Cerium Oxides: Dependence on the Effective U Parameter. Phys. Rev. B 2007, 75, 035115.
[6]
Andersson, D. A.; Simak, S. I.; Johansson, B.; Abrikosov, I. A.; Skorodumova, N. V. Modeling of $\Mathrm{}Ce{}{\mathrm{{}{}_{2}$, ${\Mathrm{{}{}_{2}{\mathrm{{}{}_{3}$, and $\Mathrm{}Ce{}{\mathrm{{}{}_{2\ensuremath{-}x}$ in the $\Mathrm{}LDA{}+U$ Formalism. Phys. Rev. B 2007, 75, 035109.
[7]
Anisimov, V. I.; Zaanen, J.; Andersen, O. K. Band Theory and Mott Insulators: Hubbard U Instead of Stoner I. Phys. Rev. B 1991, 44, 943.