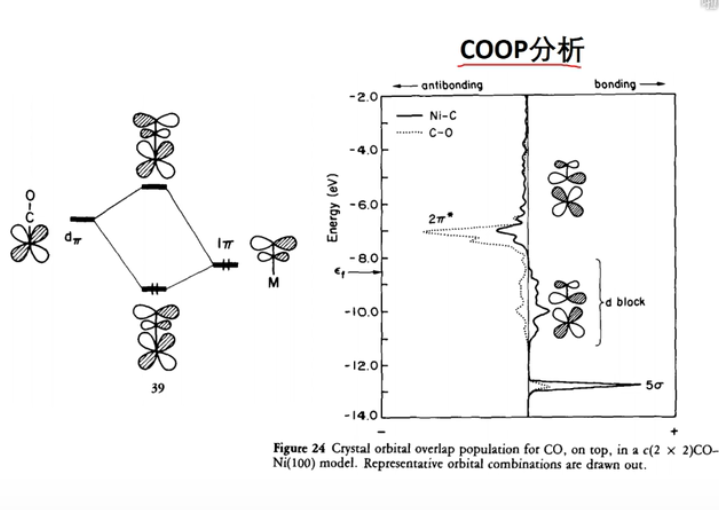
1 COOP and COHP

Both COOP (crystal orbital overlap population) and COHP (crystal orbital Hamilton population) are partitioning methods for analyzing the (k-dependent) wavefunction. While COOP partitions the electron number, COHP partitions the band structure energy. As a consequence, if you calculate the energy integral of a COOP curve, you get a number of electrons (like in the Mulliken scheme); if you integrate a COHP curve, you get an energy value that hints toward the bond strength.

• 使用LOBSTER^[1]处理VASP的输出文件(ISYM=-1,LWAVE=.TRUE.),可以得到COOP,iCOOP,COHP,iCOHP等曲线以及DOSCAR.lobster(另一种方法投影处理的DOS).

2 ELF and charge density difference (CDD)

2.1 ELF

ELF=\frac{1}{1+(\frac{D(r)}{D_h(r)})^2} where the term \frac{D(r)}{Dh(r)} normalizes the same-spin probability by the uniform-density electron gas as reference, and thus ELF is a dimensionless localization index restricted to the range of [0,1]. A high ELF value stands for a low probability of finding a second electron with the same spin in the neighboring region of the reference electron, i.e., the reference electron is highly localized.

• ELF=1: perfect localization, convalent bonding or unpaired lone electrons
• ELF=0.5: homogeneous electron gas, metallic bonding in metal
• ELF=0: totally delocalized
• Ionic bonding: low ELF area around some atoms, and high ELF area around others
• Covalent bonding: high ELF (ELF<1) area between atoms
• metallic bonding: broad high ELF(<0.6) area delocalized

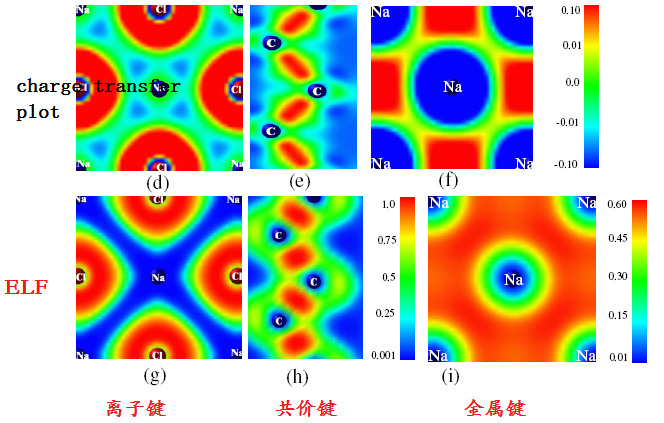
2.2 CDD

• Method 1 \Delta \rho=\rho_{A@B}-\rho_{A}-\rho_{B}

• Method 2 \Delta \rho=\rho_{All}-\sum\rho_i

3 Bader Charge Analysis^[2]

• simple combination of VASP and baderto get ACF.dat.

4 Periodic NBO^[3] and SSadNDP^[4]

• Based on Periodic NBO and SSadNDP to get multi-center bonding in Crystal.

4.1 SSadNDP Tips

1. To search 2c, 3c and 4c bonds with resonable ON values and ranges, such as set ranges relative to bond lengths.
2. Consider the symmetry, if the the number of bonds with same ON value larger than the number of left bonds, discard them and try other bonds.
3. If the bond is not localized well with atoms in (1 0 0) cell, transform them to (0 0 0) and other atoms to (-1 0 0).
4. To compare them with wannier90 WFs and VBMs in VASP partial charge density.
5. To use LREAL=.FALSE.
6. To make number in KPONTS not prime number
7. Periodic NBO could recognize 1D system, but SSAdNDP could not. To make sure the distance between images in the nonperiodic direction in the plane <0.5 nm for 1D system.

4.1.1 Visualization

1. To open lattice_vec.cube in Vesta, uncheck “show sections.”
2. Edit->Edit Data->Phase, import corresponding bonding cube file.
3. To Delete the phase with global coordinate system (uvw)=(100) and (hkl)=(001). and set the valus “This layer” of another phase to “0.5 0.5 0.5”
4. To import all phases and apply.

5 Wannier Functions

• 使用 Wannier90^[5,6]可以结合VASP计算杂化泛函和GW的相关能带和DOS计算，以及求得Wannier波函数、Fermi面以及做Boltzman输运^[7]等。

6 Bonding Estimation

• Linus Pauling proposed an empirical relationship which relates the percent ionic character in a bond to the electronegativity difference {\Delta}\chi, the percent of inoic character p_{inoic}=(1-e^{-({\Delta}\chi/2)^2})\times 100\%

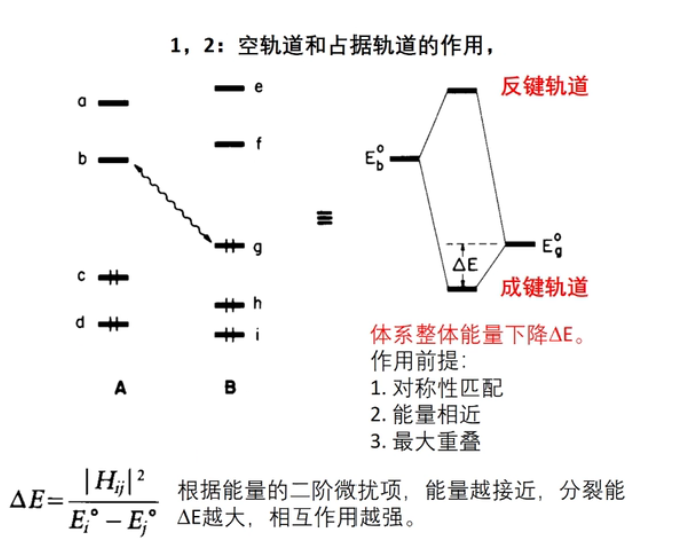
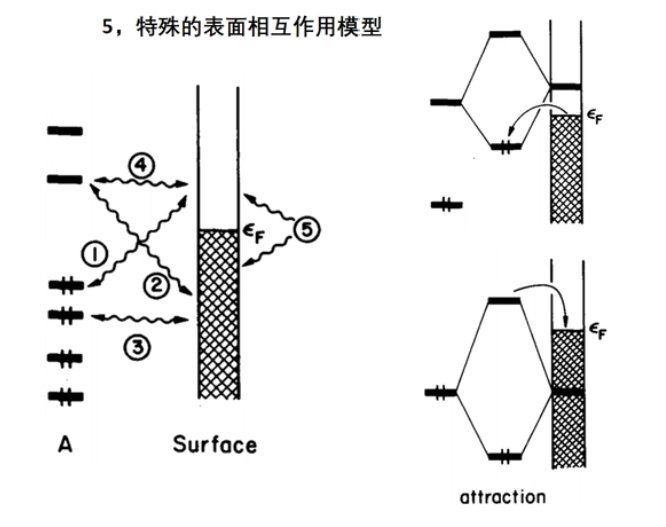
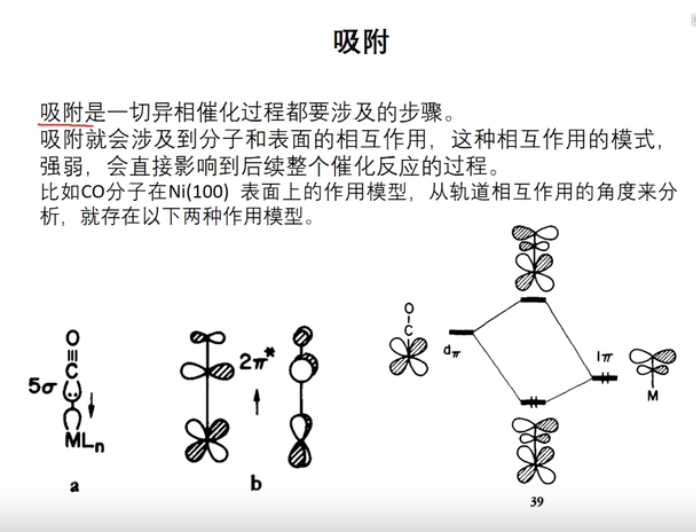
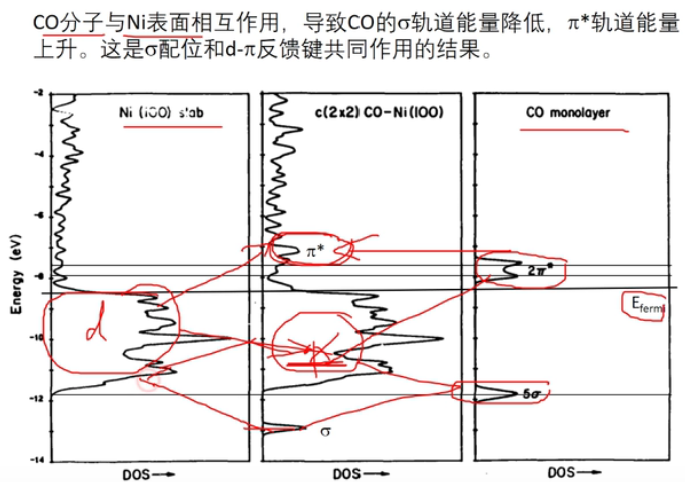
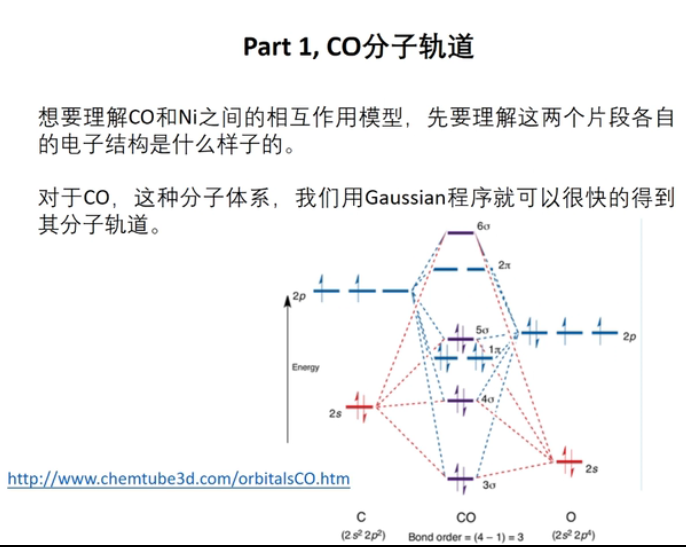
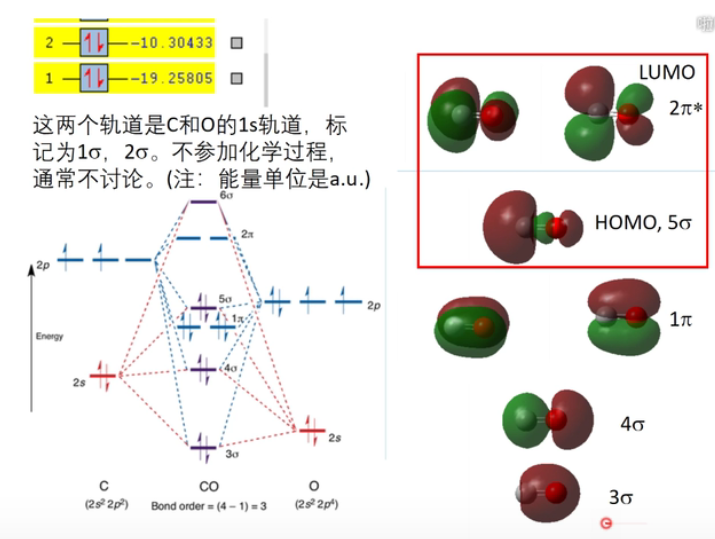
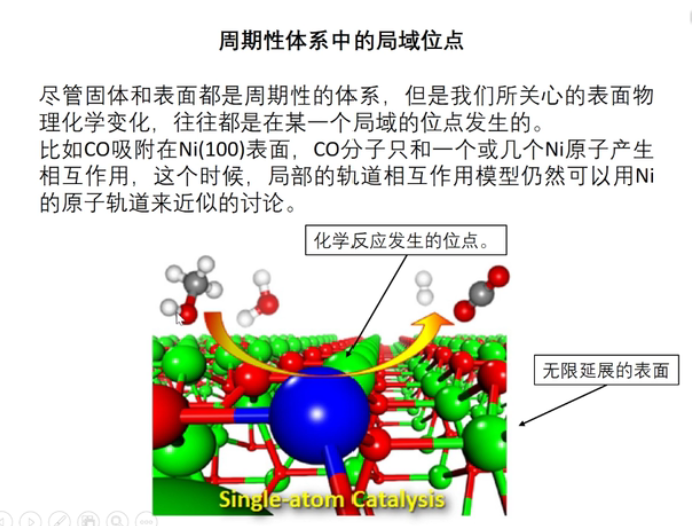
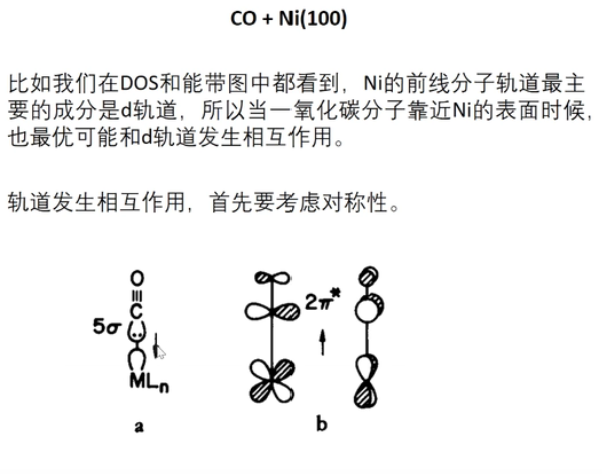
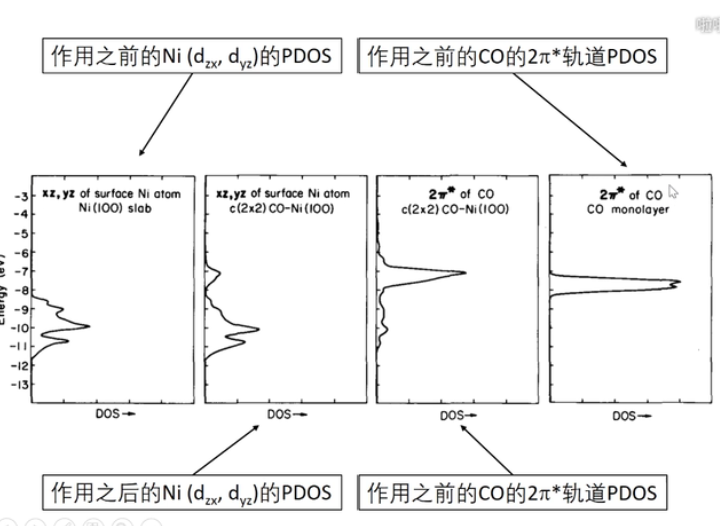
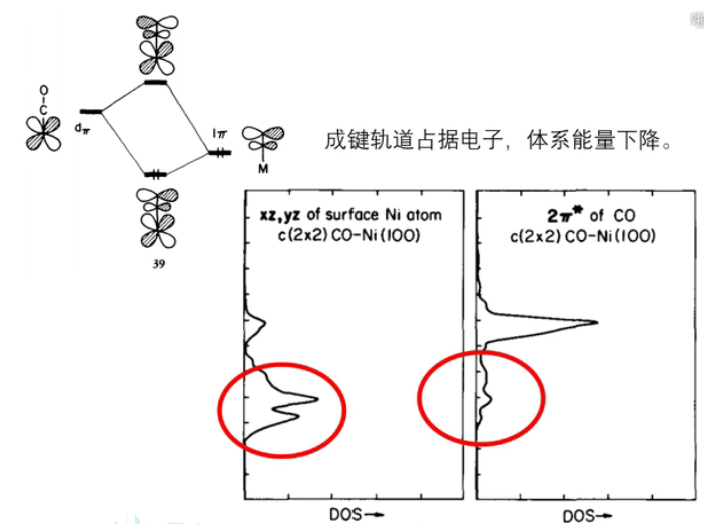
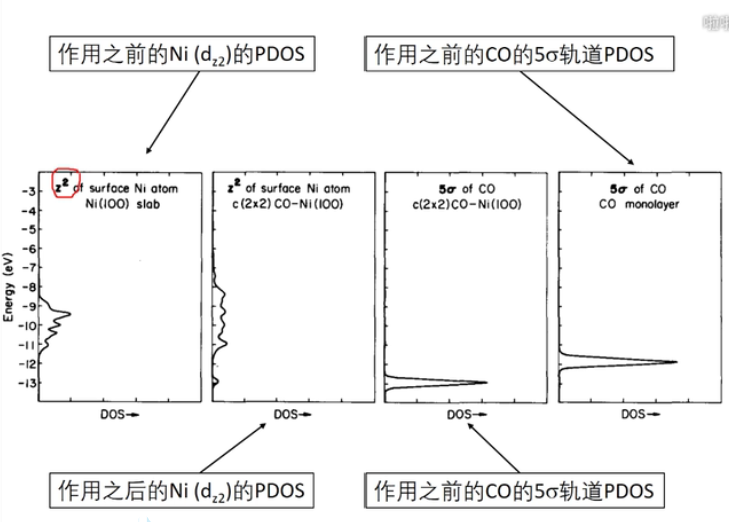
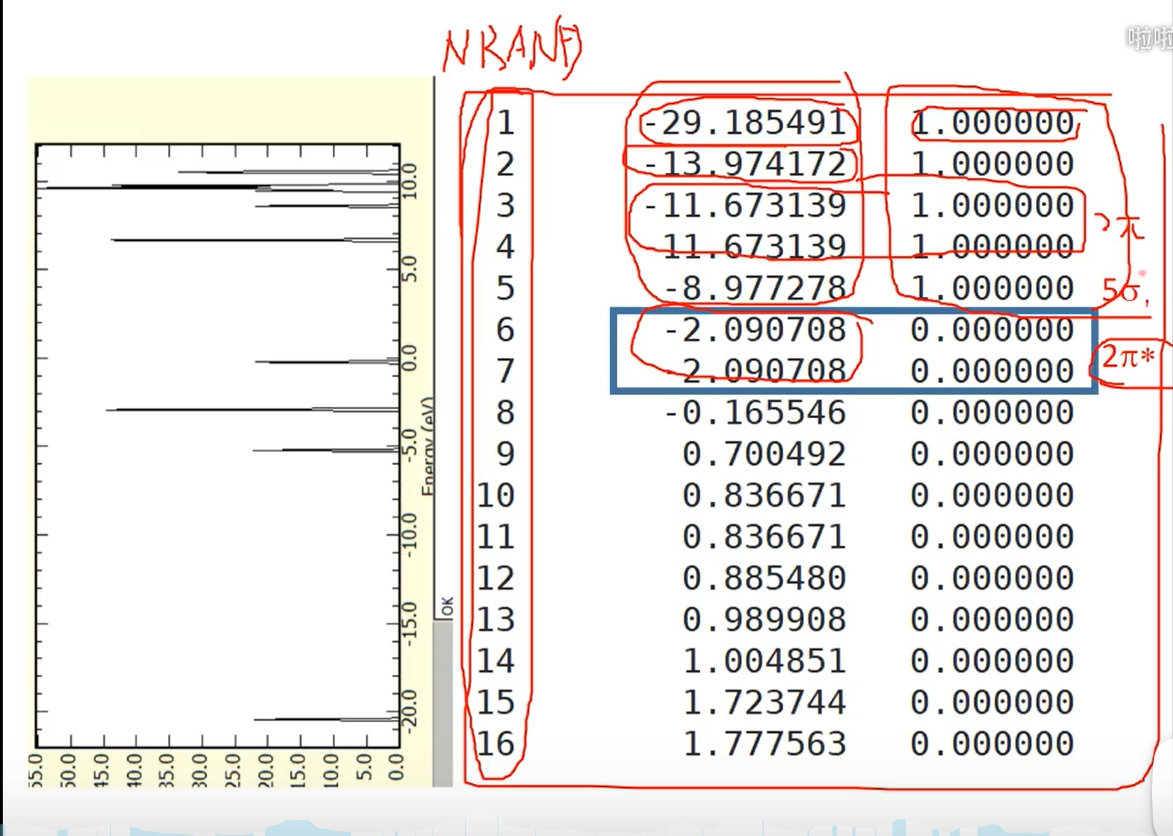
7 轨道相互作用 (From 刘锦程)

Refs:

• “Solids and Surfaces: A Chemist’s View of Bonding in Extended Structures,” Roald Hoffman
• “电子结构分析,” bilibili 刘锦程 https://space.bilibili.com/45550176