1 Theory: From H2 to Data-Storage Alloys
- From http://www.cohp.de/
The COHP (or COOP) concept is most easily understood by looking at the simple band structure of a "one-dimensional" solid; the following example has been stolen from a classic introduction. Imagine a linear chain of hydrogen atoms, the one-dimensionally periodic analogue of H2 (whose molecular-orbital scheme is known from the freshmen lecture)! Along this chain, each H atom carries one 1s atomic orbital, and we may sketch them in the following figure by colored spheres. The ideal combination of these 1s orbitals would certainly be one where all have the same plus/minus sign (visualized by like coloring); this is the H–H bonding (in-phase) crystal orbital, characterized by a positive overlap population. At high energies, we find alternating plus/minus signs between neighboring atomic orbitals; this is the H–H antibonding (out-of-phase) combination with a negative overlap population:
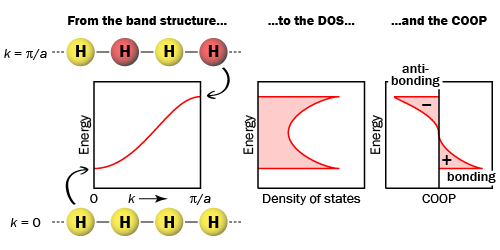
The density-of-states (DOS) diagram in the middle results as the inverse slope of the band structure on the left. Physicists will note that, funnily, quantum chemists plot the energy as a function of the DOS; while this does not make sense at all from a physicist's perspective (the DOS is a function of the energy, not vice versa), chemists want to see how the DOS emerges from the bands; it's just a matter of cultures (or religion).
A bonding indicator for the solid is easily constructed by generating an overlap population-weighted density-of-states, the crystal orbital overlap population (COOP), given on the right part of the above figure. The COOP results from multiplying the DOS by the overlap population, and it adds an additional dimension—the bonding information: it adopts positive values (bonding, because of the positive overlap population) and negative values (which identify antibonding interactions). By comparing the band structure and its orbital icons with the COOP diagram, it is obvious why the nearest-neighbor COOP is bonding at low energies and antibonding at high energies. Simple, isn't it? Note that we have effectively partitioned the electron density into bonding, nonbonding, and antibonding sections.
If one can weight the DOS by the overlap population, one can also weight it by the corresponding element of the Hamiltonian. In fact, technical reasons arising within density-functional techniques suggest to choose the latter method, dubbed crystal orbital Hamilton population (COHP). By doing so, we partition the band structure energy (instead of the electrons) but again into bonding, nonbonding, and antibonding contributions. There is also a difference in the plus/minus signs: we recall that bonding is characterized by a positive overlap population; the corresponding Hamiltonian off-site element (physicists would probably call it "hopping term") will then be negative, just like the hydrogen molecule lowers its energy by forming a bond! Consequently, antibonding interactions exhibit positive off-site Hamiltonian elements.
In order to make COHP plots look similar to COOP, most people (including us) are plotting –COHP diagrams such that bonding states (positive, to the right) and antibonding states (negative, to the left) are easy to grasp. Note that there is not a direct equivalence between COOP and –COHP—why would we need this page, otherwise?
Let us look at a more realistic example. This finger exercise, published 2002, nicely illustrates how nature optimizes structures by the above principle of maximum bonding. If one calculates the band structure of, say, elemental tellurium assuming a primitive, simple cubic crystal structure, one arrives at the following bands, DOS and COHP:
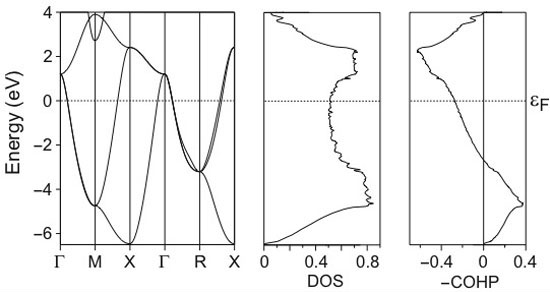
Some bands cross the Fermi level, leading to a significant DOS; cubic Te would be expected to be an electric conductor. Te–Te bonding, however, is clearly unoptimized since there are populated (!) antibonding states which lead to an enormous internal stress. As a matter of fact, more than 11 GPa pressure are needed to force tellurium into the related rhombohedral Po structure with six equal interatomic Te-Te distances; otherwise the antibonding, repelling atomic interactions cannot be counterbalanced.
Just like in molecular orbital theory, the antibonding states at high energies reflect an electronic instability, a Peierls instability in this particular case. If left alone, cubic Te immediately "explodes" and adopts its famous ground-state structure containing helices of Te atoms. You may now guess how the bands, DOS and COHP look like; here they are:
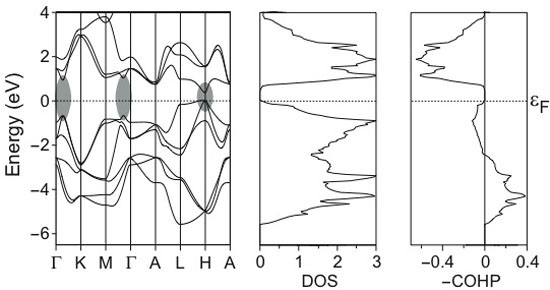
Upon structural change, a band gap opens up, depleting antibonding areas; in fact, hexagonal Te is a small band gap semiconductor, as observed in the DOS. Focusing on the COHP plots, the antibonding interactions below the Fermi level have become much smaller. Again, nature optimizes bonding.
This conceptual approach can be further extended to spin-related phenomena, offering a new look at itinerant magnetism of the transition metals. We would first like to know how the band structure of body-centered cubic (bcc) iron looks like without spin-polarization. In other words, we do a gedankenexperiment on an Fe phase which does not exist at all, namely nonmagnetic iron at zero Kelvin—here are the bands, the DOS and the Fe–Fe COHP for nonmagnetic Fe, that is, with all spins paired:
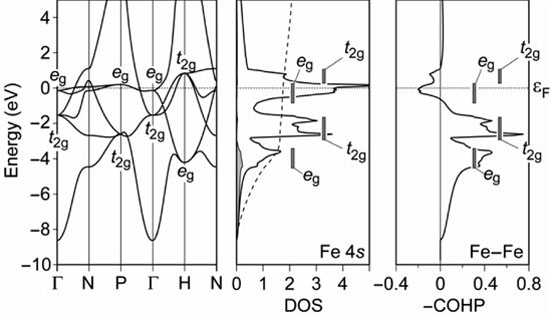
The bands in the valence region are mostly 3d, naturally, and there results the typical three-peaked DOS of a bcc transition metal. The curious thing about the nonmagnetic COHP is that the Fermi level falls in a strong Fe–Fe antibonding region. Again, we have discerned an electronic instability!
Consequently, one would expect some kind of structural change—which here does not occur: bcc-Fe stays bcc-Fe. The answer to that puzzle is that nonmagnetic iron does undergo a distortion, but instead of the atoms rearranging themselves, the electrons do. Nonmagnetic bcc-Fe is unstable with respect to an electronic structure distortion, which makes the two spin sublattices inequivalent, thereby lowering the energy and giving rise, upon ordering, to ferromagnetism; these are the corresponding spin-polarized results:
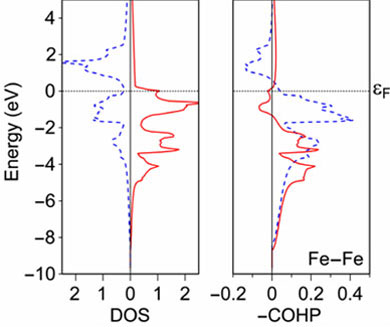
The theoretical magnetic moment (2.27 Bohr magnetons) is very close to the experimental one (2.21). Upon spin-polarization, the total energy lowers by about 0.43 eV, which is paralleled by a strengthening of the Fe–Fe bonds by roughly 5 per cent. The shifts in the majority (red) and minority (blue) spin sublattices have removed the antibonding states at the Fermi level, thereby maximizing the Fe–Fe bonding as far as possible. It looks like a new, purely electronic kind of Jahn-Teller distortion since only the electrons are involved in breaking the symmetry. What about the other transition metals? The following picture shows the nonmagnetic DOSs and metal-metal COHPs for the entire 3d row:
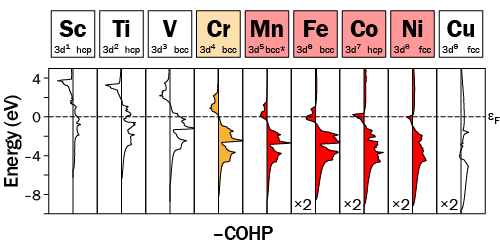
For the early transition metals like Ti, the Fermi level lies low in the COHP curve and thereby falls in the metal–metal bonding region: there is no drive towards ferromagnetism for the early transition metals. For Cr (a typical antiferromagnet), the Fermi level lies in the COHP curve between the bonding and antibonding regions, whereas for the metals from Mn (which we describe in a bcc structure for simplicity) to Ni, the Fermi level lies in the clearly antibonding region; Fe, Co, and Ni are all ferromagnetic. (To our physicist friends: yep, we know that this story can be physically explained by the size of the kinetic and exchange energies, and there is also Stoner's invaluable theory. You have, however, just witnessed a chemical interpretation of that very phenomenon.)
An extension of this idea to more complicated alloys is straightforward: if you want to synthesize a new ferromagnet, try to adjust (by chemical means such as oxidation and reduction) the Fermi energy of the material such as to push it into antibonding interactions. To avoid overloading this site, we may just refer the reader to some of the original literature.
At last, let us look at a totally different field of chemistry, in which COHP analysis has been established as quite useful as well. With the incredible amounts of digital data that are generated each day—COHP plots, stock market prices, adult movies, weather simulations—new technologies for storing such data are very much needed. A promising way is the use of so-called phase-change materials (PCMs) which can be switched between two different solid-state forms, usually a crystalline and an amporphous phase; this way, one can reversibly encode "one" and "zero" bits. Crudely sketched, it looks like this:
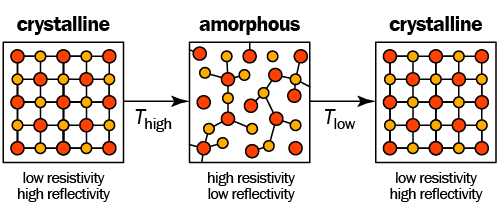
Many such PCMs are found in the ternary germanium–antimony–tellurium system. (Chemists shorten this notation to "Ge–Sb–Te", physicists and engineers are even more economic and say "GST"). Ge2Sb2Te5, for example, is found in DVD-RAM disks whereas Ge8Sb2Te11 is employed in the re-writeable Blu-Ray disk. As a first step, we here look at a few prototypical compounds but keep in mind that all "GST" materials are closely related chemically, no matter the exact stoichiometric composition.
We have now calculated COHP curves, starting with the hypothetical compound Ge2Sb2Te4 (left), taking the rocksalt structure with Ge and Sb randomly distributed on the cationic (fcc) sublattice, and Te fully occupying the other, anionic one. Indeed, this very compound does not exist; surprisingly only at first sight, it decomposes by expelling pure germanium.
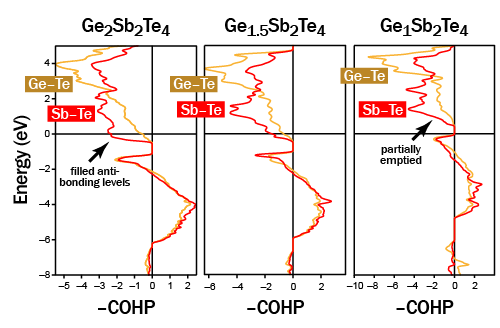
The above picture shows why. Both Ge–Te and Sb–Te bonding clearly falls into antibonding regions around the Fermi level if one starts with the fully occupied, rocksaltlike "224" phase. By removing cations (and creating vacancies on the corresponding sublattice), the Fermi level is lowered, removing electrons from these unfavorable areas. On the right, the GST-124 material is characterized where a noticeable part of these antibonding levels has been emptied, and the remaining structure is strenghtened this way. Please, as always, have a look at the original story for a more detailed presentation as possible here.